Sea ABCD un paralelogramo con ángulo obtuso en A. Sea P un punto sobre el
segmento BD de manera que la circunferencia con centro en P y que pasa por A, corte a la recta AD en A y Y , y corte a la recta AB en A y X. La recta AP intersecta a BC en Q y a CD en R, respectivamente. Muestra que ∠XPY=∠XQY+∠XRY .
Circunferencia con centro en diagonal de paralelogramo
»
- Inicie sesión o regístrese para enviar comentarios

Esta es mi solución. Sea
Esta es mi solución.
Sea ∠RQY= α, ∠QYR= β, ∠XQR= γ, ∠RXQ= θ, ∠RYP= δ, ∠PXR= ϵ.
=>∠XPY= α+β+γ+θ+δ+ϵ, ∠XQY= α+γ, ∠XRY= α+β+θ+γ y
∠XQY+∠XRY= 2α+β+2γ+θ. Entonces, si demostramos que α+γ=δ+ϵ habremos acabado. Esto lo haremos mostrando que los triángulos QYP y RYP son semejantes, análogamente lo haremos con los triángulos QPX y RPX.
Los triángulos APD y PBQ son semejantes
=> APPQ=DPPB
También los triángulos RDP y BPA son semejantes
=>PRAP=DPPB
Entonces APPQ=PRAP Pero AP=YP=XP
=>YPPQ=PRYP
XPPQ=PRXP
Luego, por el criterio de semejanza LAL,
 RYP
RYP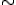
 QYP y
QYP y  RPX
RPX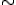
 QPX, como queríamos demostrar.
QPX, como queríamos demostrar.
b
Me parece correcta tu
Me parece correcta tu demostración. Es una demostración que usa únicamente argumentos elementales.
Por otro lado, sólo te recuerdo que la notación △ABC∼△PQR propiamente significa que el vértice A corresponde al vétice P, el B al Q; y el C al R. Esto implica que el ángulo A debe ser igual al ángulo en P e igualmente con las otras dos parejas de ángulos. Por lo que, las segmejanzas que señalas
en realidad debe escribirse así:
△RYP∼△YQP y △RPX∼△XQP
Por lo demás, tu demostración me parece elegante. ¡Felicidades!
Saludos
Cierto, Gracias por la
Cierto, Gracias por la observación y por la corrección.
No sé usar Latex, perdón
No sé usar Latex, perdón jajaja
Ya arreglé el Latex que
Ya arreglé el Latex que escribiste. Sí estaban bien tus expresiones, sólo que se te metió basura al copiar y pegar. Esto ocurre por copiar de editores con formato. Es mejor copiar y pegar de editores sin formato, como el editor de notas (notepad).