Publicaciones Recientes
XXIV Olimpiada Iberoamericana de Matemáticas (problema 3)
Sean $C_1$ y $C_2$ dos circunferencias de centros $O_1$ y $O_2$, con el mismo radio, que se cortan en $A $ y en $ B $. Sea $P $ un punto sobre el arco $AB$ de $C_2$ que está dentro de $C_1$. La recta $AP$ corta a $C_1$ en $C $, la recta $CB$ corta a $C_2$ en $D $ y la bisectriz del $\angle CAD$ intersecta a $C_1$ en $E $ y a $C_2$ en $L $. Sea $F $ el punto simétrico a $D $ con respecto al punto medio de $PE$. Demostrar que existe un punto $X $ que satisface $\angle XFL = \angle XDC = 30^\circ$ y $CX = O_1O_2$.
XXIV Olimpiada Iberoamericana de Matemáticas (problema 2)
Para cada entero positivo $ n $ se define $a_n = n+m$, donde $ m $ es el mayor entero tal que $2^{2^m}\leq n2^n$. Determinar qué enteros positivos no aparecen en la sucesión $a_n$.
XXIV Olimpiada Iberoamericana de Matemáticas (problema 1)
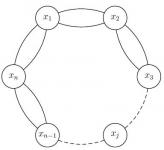
Sea $ n $ un natural mayor que 2. Supongamos que $ n $ islas están ubicadas en un círculo y que entre cada dos islas vecinas hay dos puentes como en la figura:
Olimpiada Mexicana de Matemáticas (Del. Tam. 2009): Recordatorio de entrenamiento
Les recuerdo a los 16 preseleccionados que el entrenamiento pre-norestense se llevará a cabo los días 26 y 27 (sábado y domingo) en las instalaciones de la UAMCEH-UAT.
Olimpiada Iberoamericana (el 4 de 2008)
Demuestra que no existen enteros positivos $x,y$ tales que $x^{2008}+2008!=21^y$
Olimpiada Iberoamericana (el 4 de 2004)
Determinar todas las parejas $(a,b)$, donde $a,b$ son enteros positivos de dos dígitos cada uno, tales que $100a+b$ y $201a+b$ son cuadrados perfectos de cuatro dígitos.
Olimpiada Iberoamericana (el 5 de 1985)
A cada número natural n se le asigna un entero no negativo $f(n)$ de tal manera que se satisfacen las siguientes condiciones:
- (i) $f(rs)=f(r)+f(s)$
- (ii) $f(n)=0$, si el dígito de las unidades de n es 3
- (iii) $f(10)=0$
Hallar $f(1985)$
Olimpiada Iberoamericana (el 1 de 1999)
Halla todos los enteros positivos que son menores que 1000 y cumplen con la siguiente condición: el cubo de la suma de sus dígitos es igual al cuadrado de dicho entero.
Olimpiada Iberoamericana (el 4 de 1987)
Se define la sucesión $p_n$ de la siguiente manera: $p_1=2$ y, para $n\geq2$, $p_n$ es el mayor divisor primo de $p_1p_2\ldots p_{n-1}+1$. Demostrar que $p_n$ es diferente de 5.
Sobre el significado de competencias
Noam Chomsky distinguió, en el campo de la lingüística, entre competencia y desempeño (performance). En su libro de 1965 Aspects of the Theory of Syntax, Chomsky define la competencia lingüística como el conocimiento que el individuo posee acerca de cómo hablar un idioma o lenguaje. Mientras que el desempeño lingüístico es el habla real y en contexto del individuo.
