Publicaciones Recientes
P1 OMM 1991. Fracciones con denominador 1991
Calcule la suma de todas las fracciones positivas irreducibles (simplificadas)
menores que uno y con denominador es 1991.
P6. OMM 1990. Una configuración cargada de teoría
Sea $ABC$ un triángulo rectángulo con ángulo recto en $C$. Sea $l$ cualquier recta que pase por $B$ y que corte al lado $AC$ en un punto $E$. Sean $F$ el punto medio de $EC$, $G$ el punto medio de $CB$ y $H$ el pie de la altura de $C$, respecto a $AB$, en el triángulo $ABC$. Si $I$ denota el circuncentro del triángulo $AEH$ (punto de intersección de las mediatrices de los lados), pruebe que los triángulos $IGF$ y $ABC$ son semejantes.
P5. OMM 1990. Baricentro de coordenadas enteras
Si $P_1,P_2,\ldots,P_{19}$ son diecinueve puntos del plano con coordenadas enteras tales que cada tres de ellos son no colineales, demuestre que hay tres con la propiedad de que su baricentro (punto de intersección de las medianas de un triángulo), también tiene coordenadas enteras.
P4. OMM 1990. Fichas de dominó
Considere las veintisiete fichas de dominó que quedan quitando la blanca-blanca. Tomando en cuenta los puntos que hay en una ficha, a cada ficha le corresponde un número racional menor o igual que uno. ¿Cuál es la suma de todos estos números?
P3. OMM 1990. ¿Inducción? OK ¿Pero te queda claro qué debes demostrar?
Pruebe que $n^{n-1}-1$ es divisible entre $(n-1)^2$ para todo entero $n\geq2$
P2. OMM 1990. Relación de inradios
Sea $ABC$ un triángulo rectángulo con ángulo recto en $B$, y $H$ el punto de intersección del lado $AC$ y la altura por $B$. Llamemos $r,r_1,r_2$ a los radios de las circunferencias inscritas en los triángulos $ABC,ABH,HBC$, respectivamente. Encuentre una igualdad que relacione $r,r_1,r_2$.
P1. OMM 1990. Paseos en una cuadrícula
Encuentre el total de caminos que hay del punto $A$ a línea $l$ en la red de la siguiente figura, si en un camino solo está permitido ir hacia la izquierda.
Dispositivos: experimentales de Piaget y didácticos de Brousseau
Voy a elaborar en este post (en el sentido de decir más) sobre la diferencia entre interpretar las respuestas adolescentes ante una tarea de resolución de problemas -- en términos de sus posibles razonamientos y explicando sus errores según un esquema teórico-- y hacer lo mismo pero en una situación de enseñanza.
En particular, abundaré sobre la diferencia entre los dispositivos experimentales de Jean Piaget y las situaciones didácticas de Guy Brousseau. Usaré sendos ejemplos para que el lector pueda tener una comprensión inicial de la naturaleza de los dispositivos piagetianos, y las situaciones didácticas de Guy Brousseau.
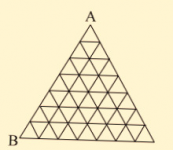
P6. OMM 1989. Trayectorias en retícula triangular
Siguiendo las líneas de la figura ¿Cuántos caminos hay para ir del punto $A$ al punto $B$ que no pasen dos veces por el mismo punto y que solo avancen hacia abajo y hacia los lados pero no hacia arriba?
P5. OMM 1989. Círculos tangentes
Sean $C_1$ y $C_2$ dos círculos tangentes de radio 1 dentro de un círculo $C$ de radio 2. Sea $C_3$ un círculo dentro de $C$ tangente a cada uno de los círculos $C,C_1,C_2$. Sea $C_4$ un círculo dentro de $C$ tangente a $C,C_1,C_3$. Demuestre que los centros de $C,C_1,C_3,C_4$ son los vértices de un rectángulo.
