Publicaciones Recientes
Quinta lección: Resolución de problemas
En este post final del curso de resolución de problemas voy a presentar 23 problemas. La solución o sugerencia se pondrá en otro post adicionada con comentarios.
Los problemas se etiquetan con A si de álgebra, con C si de combinatoria, con G si de geometría y con N si son de números. La mayoría de los problemas son elementales pero se buscó que fueran interesantes.
1N. El abuelo reparte 500 pesos entre sus 18 nietos de manera que cada nieta reciba 2 pesos menos que cada nieto. ¿Cuántas nietas tiene y cuánto les tocó en el reparto?

Algo de paridad
Demuestra que no existen soluciones enteras y positivas para la ecuacion 3m+3n+1=t2
Cuarta lección: complementos
Cuarta lección: combinatoria
En esta cuarta lección presento, a través de la regla distributiva, algunos resultados básicos de la combinatoria. En este sentido es una continuación de la lección de álgebra. A través del principio multiplicativo se derivan las fórmulas de las permutaciones y de las combinaciones o coeficientes binomiales.
Principios combinatorios en la expansión de productos
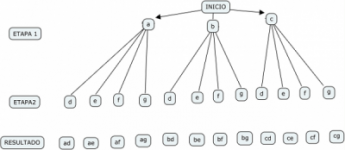
De acuerdo a la regla distributiva, en la expansión de un producto de polinomios (a+b+c)(d+e+f+g) se toman todos los productos posibles tomando un término de cada paréntesis: ad+ae+...+cf+cg.
Tercera lección: complementos
Los problemas y ejercicios que a continuación presento son de ecuaciones cuadráticas, quizá uno de los temas más avanzados de las matemáticas escolares. Ello supone que el alumno ya domina los temas más básicos asociados con la suma, resta y multiplicación de expresiones algebraicas --y las instancias de uso de la regla distributiva.
Problemas cuadráticos: completar el trinomio
El método de completar el trinomio cuadrado perfecto se puede usar para resolver ecuaciones cuadráticas. Presento enseguida un ejemplo y varios ejercicios.
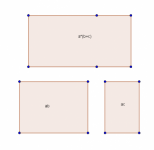
Consideremos la siguiente ecuación cuadrática: x2+10x=39.
Tercera lección: álgebra
Una de las formas de iniciar en el álgebra a los adolescentes interesados es iniciar enseñando la terminología asociada a las expresiones algebraicas (esto, obviamente con ejemplos): término, literal, coeficiente, términos semejantes, grado de un término, etc. El lector deberí
Segunda lección: complementos
En este post, dirigido a los alumnos del curso, propongo resolver 11 problemas de geometría elemental. Las dudas expresarlas en comentarios.
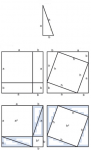
1. Encontrar la longitud de la altura de un triángulo equilátero de lado 8√21. Sugerencia:Pitágoras.
2. Utilizando el teorema de Pitágoras, demostrar que la altura de un triángulo equilátero es también mediana (y, por tanto, mediatriz y bisectriz).
Segunda lección: geometría elemental
En este post voy a relatar los temas discutidos en la segunda lección del curso de resolución de problemas que tuvo lugar en el aula C9 de la UAMCEH-UAT el sábado 16 de febrero. Se invita al usuario registrado en este curso de MaTeTaM a que visite y estudie los temas referidos ramificando su lectura hacia el link que los contiene.
Primera lección: Complementos
Una vez que se tienen los conceptos de divisibilidad y el método de agrupación de múltiplos de un número, es fácil comprender (y aprender) los criterios más usados de divisibilidad.
Criterios de divisibilidad del 3 y el 9
Si expresamos el número n en su notación decimal desarrollada, entonces es posible agrupar los múltiplos del 9 (o del 3) --mediante el artificio de ver al 1000 como 999+1-- y se hace obvia la veracidad de ambos criterios. En la discusión que sigue denotaremos con M(m) a un múltiplo cualquiera de m.
Primera lección: División con resto
El curso en resolución de problemas inició con la sesión del sábado 2 de febrero del presente, en las instalaciones de la UAMCEH-UAT y acudieron 15 alumnos. Yo inicié con el tema de divisibilidad --hasta el receso-- y Ramón lo continuó con proporciones y sistemas de numeración.
Debido a la diversidad de edades y grados (desde cuarto de primaria hasta tercero de secundaria) inicié con tres ejercicios de calentamiento para ver si dominaban la división con residuo. Afortunadamente casi todos los niños los resolvieron y así pude iniciar el tema de divisivilidad.
