Publicaciones Recientes
Un primo mayor que 3
Demostrar que 8p2+1 no es primo para ningún primo p mayor que 3.
Bisectriz en la mitad de un cuadrado
Las diagonales de un cuadrado ABCD se cortan en E, la bisectriz del ángulo DBC corta a la diagonal AC en P y al lado CD en Q. Demostrar que DQ mide el doble que PE.
Turibús
Van a viajar 27 personas en un autobús turístico que puede llevar 12 adentro y 15 afuera (en la parte superior). De las 25 personas, 5 piden ir afuera y 6 piden ir adentro. Si complacemos estas peticiones ¿de cuántas formas pueden ser distribuidas las personas en el autobús? (Considere que el orden en que se acomodan en los asientos es irrelevante, solamente importa quienes van adentro y quienes afuera.)
Un acertijo de Lewis Carroll
Un hombre camina durante 5 horas. Primero lo hace a lo largo de un tramo a nivel, después subiendo una loma. Al llegar arriba se regresa y recorre el camino a lo largo de la misma ruta pero de regreso. Caminó a 4 km/h en el camino a nivel, a 3 km/h de subida y a 6 km/h de bajada. Encontrar la distancia que recorrió.
Selección Centro OMM Tamaulipas 2014
El viernes 9 de mayo se realizó la segunda eliminatoria (concurso regional centro) del proceso de selección para la OMM Tamaulipas 2014. El concurso se celebró en las instalaciones de la UAMCEH-UAT. Los problemas son los siguientes:
1A. Un hombre camina durante 5 horas. Primero lo hace a lo largo de un tramo a nivel, después subiendo una loma. Al llegar arriba se regresa y recorre el camino a lo largo de la misma ruta pero de regreso. Caminó a 4 km/h en el camino a nivel, a 3 km/h de subida y a 6 km/h de bajada. Encontrar la distancia que recorrió.
ONMAPS Tamaulipas 2014 - Problema 10
En el interior de un triángulo ABC se elige el punto P de tal manera que los ángulos PAC y PBC son iguales. Las perpendiculares desde P a BC y CA cortan estos lados en L y M, respectivamente. Si D es el punto medio de AB, demostrar que DL=DM.
El difícil de la ONMAPS --Tamaulipas 2014
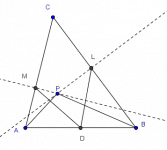
ONMAPS 2014, selección Tamaulipas
En las instalaciones de la UAMCEH-UAT se llevó a cabo el concurso de selección para la Olimpiada Nacional de Matemáticas para alumnos de secundaria y primaria. El examen consistió de 10 preguntas de respuesta abierta con valor de 7 puntos cada una. La máxima puntuación fue de 51 puntos ya la mínima de 30. Incluyo aquí las preguntas y se atacha la lista de la selección.
Concurso Municipal OMM Tamaulipas 2014
Hoy 4 de abril de 2014 se aplicó el examen del concurso municipal, primera etapa del proceso de selección de la Olimpíada Mexicana de Matemáticas en Tamaulipas. Pongo en este post los problemas con sus soluciones (algo condensadas) como una retroalimentación para los participantes.
1. En un examen de 10 preguntas, Juan las respondió todas y obtuvo 29 puntos. Si le dieron 5 puntos por cada respuesta correcta y -2 por cada incorrecta ¿cuántas preguntas respondió Juan correctamente?
Solución
El modelo algebraico es: x+y=10, 5x-2y=29. La respuesta es x=7.
Olimpiadas de matemáticas en Tamaulipas --convocatorias 2014
Este año sí vamos a iniciar el proceso de selección con más tiempo gracias a que las autoridades educativas han decidido al fin otorgarles un poco de atención. No sabemos cómo pero lo importante es que "the pennies have dropped" (los "veintes ya cayeron") en la administración estatal de la educación tamaulipeca y esperemos que en los años venideros no se atoren en el mecanismo de la SET (Secretaría de Educación de Tamaulipas).
