Publicaciones Recientes
Lista1.Problema1 (Residuo de 155/n)
El residuo que deja 80 al dividir entre un número entero positivo n es 4 ¿Cuál es residuo que deja 155 al dividirlo entre n?
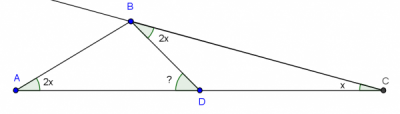
La complejidad de un problema geométrico: a propósito del 8(G) del concurso estatal
Programa de entrenamientos decidido: uno presencial y dos selectivos
Estimados preseleccionados y asesores:
Les comunico que el programa de entrenamientos y selectivos queda de la siguiente manera (entrenamientos y selectivos en las instalaciones de la UAMCEH-UAT)
Problema 5 TZALOA
Sean H,O el ortocentro y circuncentro del triangulo ABC con AB distinto de AC. Sea T la circunferencia circunscrita al triangulo ABC. La prolongacion de la mediana AM del triangulo ABC, corta a T en el punto N y la circunferencia de diametro AM corta a T en los puntos A y P. Demuestra que las rectas AP, BC y OH son concurrentes si y solo si AH=NH
Programa de entrenamientos indeciso...
Pero por lo pronto resuelvan los problemas del documento adjunto. Son 23 problemas básicos. Esperaría que no representen ningún reto para los primeros 10 lugares de la preselección (pero de cualquier manera resuélvanlos para que puedan ayudar a los restantes vía MaTeTaM).
Problema 6(C)
¿Cuántas ordenaciones (permutaciones) de las letras A,B,C,D,E,F,G no contienen los subórdenes BGE ni EAF? Ejemplo: ABCDEFG no contiene ninguno, pero CBGEAFD tiene los dos.
Problema de Cíclicos (mi primera invención)
Sea ABC un triángulo con incentro I y AB menor que AC. Sean D,E,F los puntos de tangencia del incírculo con los lados BC,CA,AB, respectivamente. Sean H la intersección de BI con EF, y G la intersección de CI con EF.
a) Demostrar que I es el incentro del triángulo DGH.
b) Demostrar que las rectas BG y CH concurren sobre la perpendicular a BC que pasa por D.
Problema 8(G)
En un triángulo ABC, el ángulo A mide el doble que el C. Se traza la mediana BD al lado CA (D es punto medio de CA). Si el ángulo DBC es igual al ángulo en A, calcular las medidas de los ángulos del triángulo ABC.
Blanchet Theorem
En un triangulo ABC donde AD es la altura (D sobre BC)sea P cualquier punto sobre AD, Y sean E,Flas intercecciones de BP,CP con AC,AB respectivamente. Entonces se cumple que AD es la bisectriz del angulo EDF
The Eyeball Theorem
Sean C1 y C2 dos circunferencias de centros A,B, respectivamente. Desde A se trazan las tangentes a AR,AS con R,S los puntos de tangencia, ademas estas rectas cortan a C1 en C,D. De la misma forma se trazan las tangentes BP,BQ a C1 con P,Q los puntos de tangencia, estas mismas cortan a C2 en E,F, respectivamente. Entonces EF=CD
