Publicaciones Recientes
Sobre la utilidad de saber trigonometría
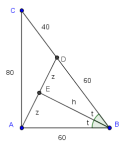
Caracterización del ortocentro
Demostrar que un punto $P$ en el interior de un triángulo acutángulo $XYZ$ es el ortocentro de éste si y sólo si
- $XP$ es perpendicular a $YZ$, y
- el reflejo de $P$ en el lado $YZ$ pertenece al circuncírculo de $XYZ$.
Método de áreas (2a parte)
En este post voy a discutir el método de áreas en el problem solving de matemáticas de concurso. El tema ya lo había discutido (un poco de manera reticente) en el post Método de áreas. En esta ocasión voy a profundizar un poco más en ese método, presentando y demostrando un teorema --y algunas de sus instancias de uso.
Suma de razones de segmentos
Sea $P$ un punto interior del triángulo $ABC$. Los rayos $AP,BP,CP$ cortan los lados $BC,CA,AB$ en los puntos $D,E,F$, respectivamente. Demostrar que
Método de áreas (revisitado)
Sean dados dos segmentos $AB$ y $PQ$, y suponga que los segmentos o sus prolongaciones se cortan en el punto $M$. Demostrar que la razón de las áreas de los triángulos $ABP$ y $ABQ$ es igual a la razón de las distancias de $P$ a $M$ y de $Q$ a $M$.
Ejercicio clásico (con descubrimiento semiguiado)
Sea $D$ un punto en la base $BC$ de un triángulo, y consideremos los triángulos $ABD$ y $ACD$.
- Demostrar que la razón de sus áreas es igual a la razón de sus bases $BD$ y $CD$.
- Demostrar que si $D$ es el punto medio de $BC$ entonces sus áreas son iguales.
- Demostrar que si $D$ es el punto en que la bisectriz del ángulo $A$ corta a la base $BC$, entonces $AB/AC=BD/CD$ (teorema de la bisectriz).
Reflexión de pies de alturas (P6)
Sea $ABC$ un triángulo acutángulo y sean $D$, $E$ y $F$ los pies de las alturas desde $A$, $B$ y $C$, respectivamente. Sean $Y$ y $Z$ los pies de las perpendiculares desde $B$ y $C$ sobre $FD$ y $DE$, respectivamente. Sea $F_1$ la reflexión de $F$ con respecto a $E$ y $E_1$ reflexión de $E$ respecto a $F$. Si $3EF = FD+DE$ demuestra que $\angle BZF_1 = \angle CYE_1$.
Nota. La reflexión de un punto $P$ respecto a un punto $Q$ es el punto $P_1$ ubicado sobre la recta $PQ$ tal que $Q$ queda entre $P$ y $P_1$, y $PQ = QP_1$
Sistema de ecuaciones en tres variable (P5)
Los números reales positivos $x$, $y$, $z$ son tales que:
$$x+ \frac{y}{z} = y + \frac{z}{x} = z + \frac{x}{y} = 2$$
Determina todos los valores posibles de $x+y+z$.
Diofantina con tres primos (P4)
Encuentra todos los enteros positivos $p$, $q$ y $r$, con $p$ y $q$ números primos, que satisfacen la igualdad:
$$\frac{1}{p+1}+\frac{1}{q+1} - \frac{1}{(p+1)(q+1)} = \frac{1}{r}$$
Desliz tras desliz te lleva a 5 (P3)
Aplicar un desliz a un entero $n \geq 2$ significa tomar cualquier primo $p$ que divida a $n$ y remplazar $n$ por $\frac{n + p^2}{p}$.
Se comienza con un entero cualquiera mayor o igual que $5$ y se le aplica un desliz. Al número así obtenido se le aplica un desliz, y así sucesivamente se siguen aplicando deslices. Demuestra que sin importar los deslices aplicados, en algún momento se obtiene el número 5.
