Publicaciones Recientes
Crónica de una sesión en problem solving
El sábado 14 de enero iniciamos Ramón Llanos y yo un curso-taller de resolución de problemas en la UAMCEH-UAT (según la idea del post 20 problemas)
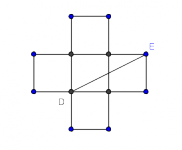
Juego de intercambios con piedras coloreadas
Sean $k$ y $n$ enteros positivos con $k\geq 2$. En una línea recta se tienen $kn$ piedras de $k$ colores diferentes. de tal forma que hay $n$ piedras de cada color. Un paso consiste en intercambiar de posición dos piedras adyacentes. Encontrar el menor entero positivo $m$ tal que siempre es posible lograr con a lo sumo $m$ pasos que las $n$ piedras de cada color queden seguidas si:
- a) $n$ es par,
- b) $n$ es impar y $k=3$
Desigualdad con multiplicadores en $\{-1,1\}$
Sean $x_1,x_2,\ldots,x_n$ números reales positivos. Demostrar que existen $a_1,a_2,\ldots,a_n\in\{-1,1\}$ tales que $$a_1x_1^2+a_2x_2^2+\ldots+a_nx_n^2\geq(a_1x_1+a_2x_2+\ldots+a_nx_n)^2$$
Ortocentro de un acutángulo
Sea $ABC$ un triángulo acutángulo con $AC\neq BC$, y sea $O$ su circuncentro. Sean $P$ y $Q$ puntos tales que $BOAP$ y $COPQ$ son paralelogramos. Demostrar que $Q$ es ortocentro de $ABC$.
Triángulo con incírculo y tres circunferencias más
Sea $ABC$ un triángulo y sean $X,Y,Z$ los puntos de tangencia de su incírculo con los lados $BC,CA,AB$, respectivamente. Suponga que $C_1,C_2,C_3$ son circunferencias con cuerdas $XY,ZX,YZ$, respectivamente, tales que $C_1$ y $C_2$ se cortan sobre la recta $CZ$ y que $C_1$ y $C_3$ se corten sobre la recta $BY$. Suponga que $C_1$ corta a las cuerdas $XY$ y $ZX$ en $J$ y $M$, respectivamente; que $C_2$ corta a las cuerdas $YZ$ y $XY$ en $L$ e $I$, respectivamente; y que $C_3$ corta a las cuerdas $YZ$ y $ZX$ en $K$ y $N$, respectivamente. Demostrar que $I,J,K,L,M,N$ están sobre una misma circunferencia.
Ecuación de inversos OIM 2011
Encontrar todos los enteros positivos $n$ para los cuales existen tres enteros no nulos $x,y,z$ tales que $x+y+z=0$ y $$\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=\frac{1}{n}$$
Por 2, por 3 o más uno
En la pizarra está escrito el número 2. Ana y Bruno juegan alternadamente, comenzando por Ana. Cada uno en su turno sustituye el número escrito por el que se obtiene de aplicar exactamente una de las siguiente operaciones: multiplicarlo por 2 o multiplicarlo por 3 o sumarle 1. El primero que obtenga un resultado mayor o igual a 2011 gana. Decidir quién tiene una estrategia ganadora y describirla.
Mesa redonda con vasijas y personas
Alrededor de una mesa redonda hay 12 personas, y sobre la mesa hay 28 vasijas. Una persona puede ver a otra si y sólo si no hay ninguna vasija alineada con ellos. Demostrar que hay por lo menos dos personas que se pueden ver la una a la otra.
Colinealidad en configuración de cíclico con ortodiagonales
Sea $ABCD$ un cuadrilátero cíclico cuyas diagonales $AC$ y $BD$ son perpendiculares. Sean $O$ el circuncentro de $ABC$, $K$ el punto de intersección de las diagonales, $L\neq O$ el punto de intersección de las circunferencias circunscritas a $OAC$ y $OBD$, y $G$ el punto de intersección de las diagonales del cuadrilátero cuyos vértices son los puntos medios de los lados de $ABCD$. Demostrar que $O,K, L,G$ están alineados.
Medias enteras
Las medias aritmética, geométrica y armónica de dos enteros positivos distintos son todas números enteros. Hallar el menor valor posible de la media aritmética de los dos enteros.
