Publicaciones Recientes
Problema 1 - IMO 2016 - Concurrencia de rectas
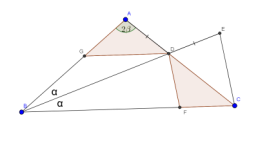
El triángulo BCF tiene ángulo recto en B. Sea A el punto en la línea CF tal que FA=FB y F se encuentra entre A y C. El punto D está elegido de tal manera que DA=DC y AC es la bisectríz de ∠DAB. El punto E es tal que EA=ED y AD es la bisectríz de ∠EAC. Sea M el punto medio de CF. Sea X el punto tal que AMXE es un paralelogramo (donde AM∥EX y AE∥MX). Demuestra que las líneas BD, FX y ME son concurrentes.
Traducido del inglés.
Resultados Examen Estatal
El día viernes 1 de julio fue la Etapa Estatal de la 30 Olimpiada Mexicana de Matemáticas en Tamaulipas. Presentaron un total de 107 alumnos de las distintas regiones del Estado. De ellos, resultaron seleccionados los siguientes 33 alumnos (en orden alfabético por nombre) que forman a la Preselección Tamaulipas 2016.
¿Seguro que sabes contar?
En un concurso de Matemáticas hay 20 participantes, alumnos de Primaria, Secundaria y Bachillerato que se sentarán en una mesa redonda. Hay igual cantidad de alumnos de Secundaria que de Bachillerato. Ya sentados se dividirán en dos equipos con cantidad par de alumnos sentados uno junto a otro (es decir, se pueden tomar de la mano todos los miembros del equipo y formarán una sola cadena). Ellos se dieron cuenta que no importa cómo se formen esos equipos, siempre habrá uno con más alumnos de Secundaria que de Bachillerato. ¿Cuántos alumnos de Primaria hay?
Circunferencia tangente a un cateto
Sea ABC un triángulo rectángulo con ∠ABC=90, BC=72, AC=78. Se considera un punto D sobre el lado AB de tal modo que 2AD=BD. Sea O el centro de la circunferencia que pasa por los puntos A y D y es tangente al lado BC. Encuentra la medida del segmento OB.
Las monedas de Ingrid
Tres triángulos que no se cortan
Considera 9 puntos sobre una circunferencia. ¿De cuántas maneras puedes dibujar 3 triángulos con vértices en estos 9 puntos, pero que no compartan vértices, de forma que ningún par de triángulos se corten?
Información para el Estatal (Preguntas Frecuentes)
Buenos días.
El día de mañana se realizará la Etapa Estatal de la Olimpiada Mexicana de Matemáticas en Tamaulipas. Estamos muy gustosos de recibir a todos los alumnos y les deseamos el mayor de los éxitos a todos.
Este en particular será uno de los Estatales más grandes que hemos tenido en Tamaulipas, recibiremos a los 108 alumnos que fueron seleccionados en las 4 regiones y a los 8 alumnos que representaron a Tamaulipas en la Olimpiada Nacional de Matemáticas para Alumnos de Primaria y Secundaria en la Cd. de México, que fue del 2 al 5 de junio, 116 alumnos en total.
Examen de prueba para el estatal
Que mejor manera de prepararse que un examen para calentar, pueden intentar hacerlo lo más parecido a un examen normal, es decir separan 4 horas de su tiempo y lo intentan resolver en ese lapso. De cualquier manera, es importante que los resuelvan. Tal vez subamos las soluciones en próximos días.
Saludos
germán
Soluciones.
Problema 1: Primero hay que responer la pregunta: ¿De cuántas maneras puedes expresar un entero n como suma de tres números sin que el primero sea cero?
Prepárate para el Estatal con MaTeTaM (Combinatoria)
Para finalizar esta serie de post me gustaría dar algunos temas para el área de combinatoria.
Técnicas de conteo: Principio aditivo y múltiplicativo, definición de factorial, combinaciones con y sin repetición, conteo con restricciones, y técnicas de conteo como contar por complementos, por casos, recursión etc.
También es conveniente tener un razonamiento a partir de modelos básicos en combinatoria como distribución de pelotas en cajas, lanzamientos de dados, recorridos en cuadrículas, dinámicas con cartas o barajas etc.
Prepárate para el Estatal con MaTeTaM (Geometria)
Siguiendo con esta serie de posts dejaré los temas importantes para el estatal, en este caso para geometria. También una lista de problemas (listageometria2016) y algunos entrenamientos, se da por sentado el tema de áreas, la lista incluye unos pocos problemas de esto pero son retadores.
No es cien por ciento necesario que aprendan a hacer demostraciones aún pero algunos problemas de geometria solo se pueden aprender si se conocen las demostraciones de algunos resultados y en que instancias se usan.
1. Ángulos entre paralelas. Hacer problemas del entrenamiento adjunto.