Publicaciones Recientes
Nietzsche, el nihilismo --y la reducción al absurdo
El último jueves del mes pasado ofrecí una charla sobre Nietzsche en la UAMCEH_UAT dentro del seminario de filosofía denominado Café y Rollos. Atacho el texto en que basé la presentación. Está en forma de cuadernillo, es decir, hay que imprimir a doble cara y después doblar a la mitad.
La parte de la charla que podría ser de interés para los lectores de MaTeTaM es la que presento en este post. Presenta el método de prueba de la reducción al absurdo con un trasfondo nihilista. Me sirvió para mostrar el lado no negativo de Nietzsche y el Nihilismo.
Problemas y resultados del V selectivo (OMM_Tam_2011)
Enseguida se presentan los problemas del quinto examen selectivo y los puntajes que los preseleccionados obtuvieron en él.
1.- Sean $A,B,C,D,E,F,G,H,I$ 9 puntos distintos en una circunferencia de radio $r$, de tal manera que $ABCD$ es un cuadrado y $EFGHI$ es un pentágono regular. Demuestra que hay un arco cuya longitud es no mayor que $\frac{\pi r}{20}$.
2. Sean $a,b,c$ 3 números enteros positivos con $(a,b)=k$ y $\frac{5a^2}{a+b}=kc$. Encuentra los posibles valores de $c$.
Sobre el concepto de frónesis en el problem solving
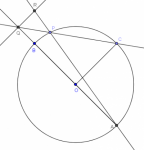
Cuarto examen selectivo OMM_Tam_2011
1. Sean $AB$ un diámetro de una circunferencia con centro en $O$, y $C$ un punto sobre ella de manera tal que $OC$ y $AB$ son perpendiculares. Considere un punto $P$ sobre el arco $BC$. Sean $Q$ la intersección de las rectas $CP$ y $AB$, y $R$ la intersección de la recta $AP$ con la recta perpendicular a $AB$ que pasa por $Q$. Demostrar que $BQ = RQ$.
2. Determina el mayor entero positivo $n$ para el cual existe una reordenación $a,b,c,d$ de los números $3,6,9,12$ de manera que
$$\sqrt[n]{3^a\times6^b\times9^c\times12^d}$$
es un entero.
PISA: pensar la educación matemática de otra manera
Parece ser que los escuelantes y los profesores de secundaria y bachillerato han sido tomados por sorpresa por los exámenes ENLACE, PISA y CENEVAL. Y más sorprendidos están los administradores educativos desde los expertos de la SEP hasta los directores de escuela (pasando por los líderes sindicales). Pues la consigna, no expresada pero vigente, de los administradores es: que todos pasen, así se tengan que inflar las calificaciones.
Selección norestense, Tamaulipas 2011
A petición del delegado Tamaulipas de la Olimpiada Mexicana de Matemáticas, se publican enseguida los resultados finales de los tres exámenes selectivos aplicados a los 25 seleccionados en la etapa estatal de la Olimpiada Mexicana de Matemáticas (Delegación Tamaulipas) --celebrada el día 9 de septiembre de 2011 en las instalaciones de la UAMCEH-UAT.
Los 15 alumnos de mayor puntuación participarán en la Olimpiada Norestense de Matemáticas que se efectuará los días 20, 21 y 22 de octubre de 2011 en la ciudad de Saltullo, Coahuila.
Resultados (y problemas) del examen selectivo 3 OMM_Tam_2011
La suerte está echada. Hagan sus cuentas.
Los problemas del segundo selectivo OMM_Tam_2011
Estos son los problemas de teoría de números del segundo examen selectivo para la preselección Tamaulipas OMM 2011.
Problema 1. Demostrar que $p^2-1$ es divisible entre 24 si $p$ es un primo mayor que 3.
Problema 2. Encontrar todas las ternas de núumeros enteros $(a, b, c)$ que cumplen
\begin{eqnarray}
ab + bc &= 44\\
ac + bc &= 23
\end{eqnarray}
Problema 3. De los números positivos que pueden ser expresados como suma de 2005 enteros consecutivos, no necesariamente positivos ¿cuál ocupa la posición 2005?
Problema 4. Demostrar que si $n$ es múltiplo de 3, entonces $2^n-1$ es divisible entre 7.
Puntajes del segundo selectivo (OMM Tamaulipas 2011)
Los siguientes son los puntajes del segundo selectivo que envió Orlando Ochoa Castillo.
Estructura de los problemas de variación inversa
En este post voy a presentar la cuestión de que si el alumno no cumple los pre-requisitos para estar en un cierto nivel escolar, entonces la educación se convierte en una farsa. Porque, siendo realistas, el profesor no tomará medidas remediales para sus alumnos más débiles. En primer lugar porque el tiempo del aula es un recurso escaso. En segundo lugar porque interpretará los excesivamente laxos filtros de entrada de la administración escolar como un insulto a su profesión. (Un primer pre-requisito es ¿sabe leer? --¿es esto mucho pedir?).
