Publicaciones Recientes
El polo de la recta que pasa por el vértice y el punto de tangencia.
Sea ABC un triángulo y sean D, E y F los puntos donde la circunferencia circunscrita es tangente al lado BC, CA y AB. Llamemos D′ el punto donde la recta EF corta a la recta AB. Demuestra que:
a) D′ es el conjugado armónico de D con respecto al segmento AB.
b) Que la recta AD es la polar de D′ respecto al incírculo.
Demostrar cuadrado
Sea ABCD un cuadrilatero tal que los angulos internos en los vertices A, B, y C son de cuarenta y cinco grados. Demostrar que los puntos medios de los lados del cuadrilatero determinan un cuadrado.
Propuesto por: Fernando
Clasificación de primos que dividen a un cuadrado más uno
Demuestra que si p es un primo impar que divide a n2+1 para algún n, entonces p debe ser de la forma 4k+1, es decir, p≡1 (mód 4).
Media armónica de las bases de un trapecio.
Considere μ un segmento paralelo a las bases a y b de un trapecio, de tal manera que μ pasa por el punto de intersección de las diagonales y sus extremos están sobre los lados del trapecio. Demostrar que μ es la media armónica de a y b, es decir:
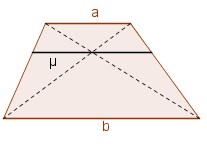
No es un cuadrado perfecto
Demostrar que si y es un entero, 187y−1 no es un cuadrado perfecto.
¿Cómo subir imágenes a MaTeTaM?
División anular
Sean a,b,c tres números enteros positivos tales que a divide a b2, b divide a c2 y c divide a a2. Demostrar que abc divide a a7+b7+c7.
Tres círculos congruentes
Tres círculos C1,C2,C3 del mismo radio se intersectan no tangencialmente en un punto P. Sean A,B los centros de C1,C2, respectivamente; y C,D los puntos de intersección de C1,C2, respectivamente, con C3. (C,D son ambos diferentes de P.) Demostrar que ABCD es un paralelogramo.
Desigualdad de las medias --con un max-min-razonamiento
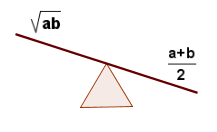
¿Qué teoremas se valen de conjugados armónicos en la olimpiada?
Brandon me comentó en el problema "Bisectriz, ángulo recto y conjugados armónicos" lo siguiente:
