Blog de jmd
Inferencias elementales a partir de la congruencia de ángulos
Este post, al igual que el anterior, se inscribe en la Reforma al Bachillerato (Bloque I, Matemáticas II). En él voy a elaborar (discutir) sobre los procesos de inferencia que pueden realizarse en configuraciones geométricas muy básicas, utilizando el concepto de ángulos congruentes. Y algunos resultados muy básicos, como el de la suma de los ángulos interiores de un triángulo, las relaciones de complementariedad y suplementariedad de dos ángulos.
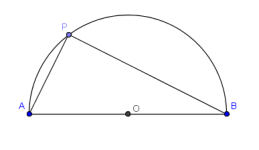
Clasificación de ángulos
Parecería que de ángulos hay muy poco que decir. Son los objetos geométricos que se miden con un transportador ¿cierto? Cierto, pero hay toda una terminología escolar que el aprendiz debería aprender.
En lo que sigue voy a hablar primero de una clasificación de los ángulos, y en la segunda parte voy plantear la clasificación de las relaciones entre dos ángulos. En cada una de esas clasificaciones se presenta primero un mapa conceptual y después se hace el mismo planteamiento pero de manera discursiva.
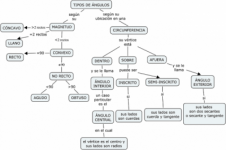
Sentido de la estructura geométrica
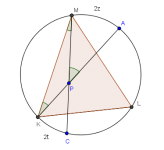
Dispositivos: experimentales de Piaget y didácticos de Brousseau
Voy a elaborar en este post (en el sentido de decir más) sobre la diferencia entre interpretar las respuestas adolescentes ante una tarea de resolución de problemas -- en términos de sus posibles razonamientos y explicando sus errores según un esquema teórico-- y hacer lo mismo pero en una situación de enseñanza.
En particular, abundaré sobre la diferencia entre los dispositivos experimentales de Jean Piaget y las situaciones didácticas de Guy Brousseau. Usaré sendos ejemplos para que el lector pueda tener una comprensión inicial de la naturaleza de los dispositivos piagetianos, y las situaciones didácticas de Guy Brousseau.
Sentido de la estructura algebraica
En el paper Developing Katy's Algebraic Structure Sense, Hoch y Dreyfus, los autores de este reporte de investigación, someten a prueba empírica un método de enseñanza individualizada de las matemáticas que podríamos llamar "entrevistas didácticas" (teaching interviews).
Los autores usan las entrevistas didácticas para mejorar el desempeño en matemáticas de adolescentes que, si bien son buenos en la manipulación algebraica, no han adquirido el "sentido de la estructura". Eligieron para ilustrar los resultados a Katy, una adolescente de 16 años.
Si tienes la teoría, la práctica es más eficaz
El problema 1 del concurso estatal
Demostrar que el número 100...001, el cual tiene doscientos ceros intermedios, es múltiplo de 1001
pone en juego uno de los conocimientos más elementales de las matemáticas escolares: el significado de "múltiplo" y el algoritmo de la división. No se necesita más para resolverlo.
El método directo es emprender la división entre 1001. Pero son muchas cifras... tantas que no caben todas en la hoja de papel. ¿Entonces? Bueno, lo que está obligado a hacer el cognizador es a idear una estrategia alternativa.
Método de áreas (para encontrar razones)
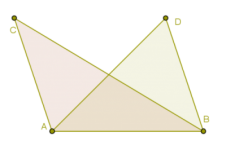
Sobre el significado de intuición
Hace algún tiempo escribí sobre la paradoja denominada de Monty Hall (Ver mi post Hagamos un trato.) Esa paradoja es paradoja precisamente porque la intuición falla en dar una solución correcta.
En lo que sigue, añado otras dos paradojas para demostrar la falibilidad de nuestra intuición. (Disclaimer: no es una tacha a la intuición, es solamente el reconocimiento de que puede fallar --"no la quiero perfecta, me basta con que funcione la mayoría de las veces")
Torres de Hanoi: un ejemplo de juego reglado
Las Torres de Hanoi es un acertijo matemático que consiste de tres postes y varios discos de diferente diámetro con un orificio central, de manera que se puedan ensartar en los postes. Es un juego reglado --muy útil para adquirir la disciplina de jugar de acuerdo a unas reglas... y para otras proficiencias en el problem solving.

Trasquilar la borrega... ¿te hace sentido?
Seguramente la frase "trasquilar la borrega" no te hace sentido pero... quizá al terminar de leer este post le puedas atribuir un sentido...
Este domingo que pasó me desperté con la idea de ponerme a escribir un post para MaTeTaM sobre el último grito de la moda en educación matemática o, mejor dicho, en didáctica de las matemáticas (por lo menos en USA), denominado reasoning and sense making, pues entre semana había navegado un poco en la Web investigando sobre la guerra de las matemáticas (Math Wars) en Estados Unidos.
