Avanzado
5.- Borrando divisores de un pizarrón
Sea n>1 un entero positivo y sean d1<d2<...<dm sus m enteros positivos de manera que d1=1 y dm=n. Lalo escribe los siguientes 2m números en un pizarrón:
d1,d2,...,dm,d1+d2,d2+d3,...,dm−1+dm,N
donde N es un entero positivo. Después Lalo borra los números repetidos (por ejemplo, si un número repetido aparece 2 veces, el borrará uno de los dos). Después de esto, Lalo nota que los números en el pizarrón son precisamente la lista completa de divisores positivos de N. Encuentra todos los posibles valores del entero positivo n.
3.- Orquesta Matemática
Sea n>1 un entero y sea d1<d2<⋯<dm la lista completa de sus divisiores positivos, incluidos 1 y n. Los m instrumentos de una orquesta matemática se disponen a tocar una pieza musical de m segundos, donde el instrumento i tocará una nota de tono di durante si segundos (no necesariamente consecutivos), donde di y si son enteros positivos. Decimos que esta pieza tiene sonoridad S=s1+s2+⋯+sm.
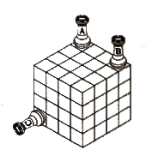
2.- Ataque de torres en un tablero cúbico.
Sea n un entero positivo. David tiene 6 tableros de ajedrez de n×n que ha dispuesto de manera que formen las 6 caras de un cubo de n×n×n. Se dice que dos casillas a y b de este nuevo tablero cúbico están alineadas si podemos conectarlas por medio de un camino de casillas a=c1,c2,…,cm=b de manera que cada pareja de casillas consecutivas en el camino comparten un lado, y los lados que la casilla ci comparte con sus vecinas son lados opuestos del cuadrado ci, para i=2,3,…,m−1. Diremos que dos torres colocadas sobre el tablero se atacan; si las casillas que ocupan están alineadas. David coloca algunas torres sobre el tablero de forma que ninguna ataque a otra.
Problema 5 - IMO 2022 - Redacción corta pero peligrosa
Hallar todas las ternas (a,b,p) de números enteros positivos con p primo que satisfacen
ap = b! + p
Secuencia de conjuntos no vacios (OMM 2021 P6)
Determina todos los conjuntos no vacíos C1,C2,C3,…, tales que cada uno de ellos tiene un número finito de elementos y todos sus elementos son enteros positivos, con la siguiente propiedad: Para cualesquiera enteros positivos m y n, la cantidad de enteros positivos en el conjunto Cm más la cantidad de enteros positivos en Cn es igual a la suma de los elementos en el conjunto Cm+n.
Nota: Al denotar con |Ck| la cantidad de elementos de Ck y con Sk la suma de los elementos de Ck, la condición del problema es que para m , n enteros positivos se cumple
|Cn|+|Cm|=Sm+nNúmeros digitales (OMM 2021 P5)
Para cada entero n>0 con expansión decimal ¯a1a2…ak definimos s(n) como sigue:
- Si k es par, s(n)=¯a1a2+¯a3a4+⋯+¯ak−1ak
- Si k es impar, s(n)=a1+¯a2a3+¯a4a5+⋯+¯ak−1ak
Por ejemplo, si n=123 entonces s(n)=1+23=24 y si n=2021 entonces s(n)=20+21=41.
Decimos que este n es digital si n es múltiplo de s(n). Muestra que entre cualesquiera 198 enteros positivos consecutivos, todos ellos menores que 2000021, hay uno de ellos que es digital.
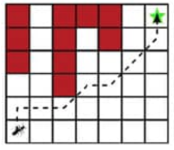
La hormiga, el mago y la lava (OMM 2021 P3)
Sean m,n≥2 dos enteros. En una cuadrícula de m×n, una hormiga empieza en cuadrito inferior izquierdo y quiere camina al cuadradito superior derecho. Cada paso que da la hormiga debe ser a un cuadrito adyacente, de acuerdo a las siguientes posibilidades ↑, → y ↗. Sin embargo, un malvado mago ha dejado caer lava desde arriba y ha destruido algunos cuadritos de forma tal que:
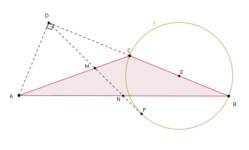
Es punto medio si y sólo si el otro es punto medio (OMM 2021 P2)
Sea ABC un triángulo tal que ∠ACB>90∘ y sea D el punto de la recta BC tal que AD es perpendicular a BC. Considere Γ la circunferencia de diámetro BC. Una recta que pasa por D es tangente a la circunferencia Γ en P, corta al lado AC en M (quedando M entre A y C) y corta al lado AB en N.
Demuestra que M es punto medio de DP si, y sólo si N es punto medio de AB.
Problema 1 - IMO 2019 - Determinar todas las función enteras.
Sea Z el conjunto de los números enteros. Determinar todas las funciones f:Z→Z tales que, para todos los enteros a y b, f(2a)+2f(b)=f(f(a+b)).
El seis de la ORO. (Paisanos)
Un cambio para un número natural n consiste en agregar una pareja de ceros entre dos dígitos o al final de la representación decimal de n. Un paisano de n es un número que se puede obtener haciendo uno o más cambios en n. Por ejemplo 40041 y 44001 son paisanos de 441. (Nota: 441 no es paisano de 44100). Determina todos los números naturales n para los cuales existe un número natural m con la propiedad de que n divide a m y a todos los paisanos de m.
