Intermedio

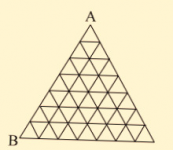
Siguiendo las líneas de la figura ¿Cuántos caminos hay para ir del punto $A$ al punto $B$ que no pasen dos veces por el mismo punto y que solo avancen hacia abajo y hacia los lados pero no hacia arriba?
 

Encuentre el entero positivo mas pequeño $n$ tal que, si su expansión decimal es $n=a_ma_{m-1}\ldots{a_2}a_1a_0$ y $r$ es el número cuya expansión decimal es $r=a_1a_0a_ma_{m-1}\ldots{a_2}0$, entonces $r$ es el doble de $n$.
 

Pruebe que no existe un número positivo de 1989 cifras que tenga al menos tres de ellas iguales a 5 y tal que la suma de todas las cifras sea igual al producto de las mismas.

Encuentre dos números enteros $a$ y $b$ tales que:

• $b^2$ es múltiplo de $a$;
• $a^3$ es múltiplo de $b^2$;
• $b^4$ es múltiplo de $a^3$;
• $a^5$ es múltiplo de $b^4$;
• pero $b^6$ no es múltiplo de $a^5$.

Considere un triángulo $ABC$ en el que la longitud del lado $AB$ es 5, las medianas por $A$ y por $B$ son perpendiculares entre sí y el área es 18. Hallar las longitudes de los lados $BC$ y $AC$.

Calcule el volumen del octaedro que circunscribe a una esfera de radio 1.
 

Si $A$ y $B$ son subconjuntos ajenos del conjunto $\{1,2,\ldots,m\}$ y la suma de los elementos de $A$ es igual a la suma de los elementos de $B$, pruebe que el número de elementos de $A$ y también de $B$ es menor que $m/\sqrt{2}$
 

Si $a$ y $b$ son dos enteros positivos primos relativos y $n$ es un entero, pruebe que el máximo común divisor de $a^2+b^2-nab$ y $a+b$ divide a $n+2$

¿Cuántas maneras hay de escoger ocho enteros $a_1,a_2,a_3,\ldots,a_8$ no necesariamente distintos, tales que $1\leq{a_1}\leq\ldots\leq{a_8}\leq8$?
 

Si $a$ y $b$ son enteros positivos, pruebe que 19 divide a $11a+2b$ si y sólo si 19 divide a $18a+5b$