Problemas - Álgebra
Suma algebraica
La suma de 4020 números enteros consecutivos es 2010. Encontrarlos.
Abuelo, nietos y domingo
El abuelo repartió 500 pesos entre sus 18 nietos de manera que cada niña recibió 2 pesos menos que cada niño. ¿Cuánto recibió cada quien en el reparto?
Fracción con mínimo denominador
De todas las fracciones $\frac{x}{y}$ que cumplen $$\frac{41}{2010}<\frac{x}{y}<\frac{1}{49}$$ encuentra la que tenga menor denominador.
Seccionado recursivo
Sofía tiene 5 pedazos de papel en una mesa. Toma algunos de los pedazos, corta cada uno en 5 pedacitos y los vuelve a poner en la mesa. Ella repite este procedimiento varias veces hasta que se cansa. ¿Podría Sofía llegar a tener 2010 pedazos al final en la mesa?
Suma de potencias múltiplo de 7
Demostrar que para $n$ entero no negativo, la función $f(n)=4^{2^n}+2^{2^n}+1$ es múltiplo de 7.
Coeficientes de una expresión cuártica
Calcular el valor de la expresión $(a_0+a_2+a_4)^2-(a_1+a_3)^2$, donde los $a_i$ son los coeficientes de la expansión de $(2x+\sqrt{3})^4$: $$(2x+\sqrt{3})^4=a_0+a_1x+a_2x^2+a_3x^3+a_4x^4$$
Desigualdad de Jensen
Sea $f:\mathbb{R} \to \mathbb{R}$ una función punto medio convexa, es decir, que satisface que: $$f\left( \frac{x+y}{2} \right) \leq \frac{f(x)+f(y)}{2} $$ para toda pareja de números reales $x,y \in \mathbb{R}$.
Demostrar que para cualesquiera números reales $a_1, a_2, \ldots, a_n$ se satisface la siguiente desigualdad: $$f \left(\frac{a_1+a_2+ \cdots +a_n}{n} \right) \leq \frac{f(a_1)+f(a_2)+\cdots +f(a_n)}{n}.$$
Composición de la función "suma de sus dígitos"
Para un entero positivo $ n $ se definen $n_1$ como la suma de los dígitos de $ n $, $n_2$ como la suma de los dígitos de $n_1$, y $n_3$ como la suma de los dígitos de $n_2$.
Por ejemplo para $n = 199$, $n_1 = 199_1 = 19, n_2 = 199_2 = 10$ y $n_3 = 199_3 = 1$.
Encuentra todas las parejas de enteros positivos $(m, n)$ tales que:$$m + n = 2007$$ $$m_3 + n_3 = 2007_3$$
Desigualdad homogenea
Sean $a, b, c$ números reales positivos que satisfacen $a+b+c = 1$.
Muestra que: $$\sqrt{a + bc} + \sqrt{b + ca} + \sqrt{c + ab}\leq 2.$$
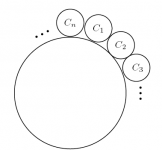
Juego de caballeros
Los caballeros $C_1,C_2,\ldots,C_n$, del Rey Arturo, se sientan en una mesa
redonda de la siguiente manera:
El rey decide realizar un juego para premiar a uno de sus caballeros. Iniciando con $C_1$, y avanzando en el sentido de las manecillas del reloj, los caballeros irán diciendo los números 1, 2, 3, luego 1, 2, 3, y así sucesivamente (cada caballero dice un número). Cada caballero que diga 2 ó 3 se levanta inmediatamente y el juego continúa hasta que queda un solo caballero: el ganador.