Álgebra
P7. El orden de x, y y z es independiente de a y b.
Supongamos que a y b son dos números reales tales que 0<a<b<1. Sean :
x=1√b−1√a+b,y=1b−a−1byz=1√b−a−1√bMuestra que x, y y z quedan siempre ordenados de menor a mayor de la misma manera, independientemente de la elección de a y b. Encuentra dicho orden entre x, y y z.
P4. Encuentra todas las asignaciones f(m,n)
1.- Números Tlahuicas
Un número x es Tlahuica si existen números primos distintos p1,p2…,pk tales que
x=1p1+1p2+...+1pkDetermina el mayor número Tlahuica que satisface las dos propiedades siguientes:
- 0 < x < 1
- existe un número entero 0<m≤2022 tal que mx es un entero.
El 6 del último selectivo 2022
Se definen las sucesiones xn y yn mediante las siguientes reglas:
- x0 = 2, x1 = 5, xn+1 = xn + 2xn-1
- y0 = 3, y1 = 4, yn+1 = yn + 2yn-1
Demuestra que no hay números que estén en ambas sucesiones.
Sin miedo al factorial
Determina el menor entero positivo n tal que para todo entero positivo u se cumple que n + u! sea un número de al menos 4 divisores
Promedio de un colección de m números
a) Demuestra que si a una colección de m números le agregamos su promedio, la nueva colección de m+1 números tendrá el mismo promedio.
b) Demuestra que el promedio de una colección de m números es menor o igual a su número más grande, y mayor o igual a su número más pequeño.
El número de Belmaris
André, Belmaris, Claudia, Daniel, Elmer y Germán van a jugar a decir números en ese orden. André y Belmaris podrán elegir sus números, pero los siguientes deben decir el resultado de la multiplicación de los números que dijeron las dos personas antes que ellos, sin equivocarse. Si André dijo "2" y Germán dijo "6 075 000" (seis millones setenta y cinco mil), ¿qué numero dijo Belmaris?
Problema 5 - IMO 2022 - Redacción corta pero peligrosa
Hallar todas las ternas (a,b,p) de números enteros positivos con p primo que satisfacen
ap = b! + p
Los favoritos de Claudia
Claudia escribe una lista de sus 11 números favoritos más pequeños. El primero es el 5 y el tercero es 13, además, se dió cuenta que todos los números excepto el primero y el último resultan ser el promedio de los dos números que tiene a lado. ¿Cuál es el último número de su lista?
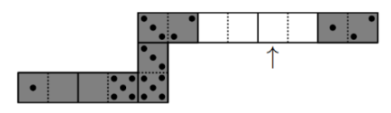
Fichas de dominó
Pancho hizo una hilera con 7 fichas de dominó de manera que los lados con el mismo número de puntos quedaron uno al lado del otro. Originalmente la hilera tenía un total de 33 puntos, pero el hermanito de Pancho se llevó dos de las fichas. ¿Qué cantidad de puntos había en el lugar que señala la flecha en la figura?