Geometría
Encontrar ángulo dada una bisectriz
En un rectángulo ABCD, F es el punto medio del lado CD y E es un punto del lado BC tal que AF es bisectriz del ángulo EAD. Si el ángulo AEF mide 68 grados ¿cuál es la medida del ángulo BAE?
Los problemas del nacional de la 12 ONMAS
Área de pentágono
Por los vértices D y A del cuadrado ABCD de lado 5 se trazan, respectivamente, los segmentos paralelos DE y AF hacia afuera del cuadrado, de tal manera DE mide 4 y es perpendicular a EF. Encuentra el área del pentágono ABCEF.
Demostrar perpendicular
Sean ABC un triángulo rectángulo y M el punto medio de la hipotenusa BC. Sus catetos cumplen que CA es menor que AB. Se coloca un punto D sobre AB de manera que CA=AD. Finalmente, sea E el punto común de AM y CD. Si F es un punto sobre BC tal que EF es paralela a BC AC, demostrar que AM es perpendicular a FD.
Tangentes a circunferencia desde el centro de otra
Considere las circunferencias a y b de centros A y B respectivamente. Desde el centro A se trazan las tangentes a b y éstas cortan a a en los puntos P y Q. Desde el centro B se trazan las tangentes a a que cortan a b en R y S. Demostrar que PQRS es un rectángulo.
Círculo de diámetro la base de un triángulo
Sea ABC un triángulo tal que la circunferencia S de diámetro BC pasa por el punto medio M de AB. Sea N un punto sobre S de manera que MN es diámetro de S. Probar que el área del triángulo ABC entre el área del triángulo MNC es 2.
Razón de áreas
En el rectángulo ABCD, los puntos P,Q,R,S, uno en cada lado, dividen el lado donde están en razón 3:2. ¿Cuál es el cociente del área del paralelogramo PQRS entre el área de la región del rectángulo que queda afuera del paralelogramo? (N del E: en el examen se dio la figura.)
Demostrar paralelogramo
Sean ABCD un paralelogramo, y P,Q,R,S puntos exteriores a él. M1 y M2 son puntos medios de PA y AQ, respectivamente, y G1 la intersección de QM1 y PM2. (G1 es el gravicentro del triángulo PAQ). De la misma manera se localizan los puntos G2,G3,G4 en los triángulos QRB,RSC y SPD, respectivamente. Demuestre que G1G2G3G4 es un paralelogramo.
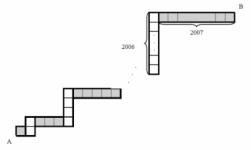
2007 ONMAS escalera
Tengo 2007 rectángulos de dimensiones 1×1,1×2,1×3,…,1×2007 y los coloco en ese orden poniendo uno horizontal, luego otro vertical, etc. (como se muestra en la figura) formando una escalera.
¿Cuánto mide el segmento que va desde el punto A hasta el punto B?
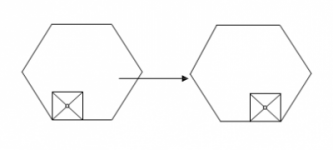
Cuadrado deslizante en hexágono
En la esquina inferior izquierda de un hexágono regular de lado 4 metros se coloca un cuadrado de lado 2 metros, tal y como se observa en la parte izquierda de la figura.
El cuadrado “rueda” (sin deslizarse) sobre los lados del hexágono y por la parte interior de éste, girando en el sentido inverso de las agujas del reloj y manteniendo siempre un vértice apoyado en un lado del hexágono (el primer movimiento aparece en la figura). Cuando el punto P --que es la intersección de las diagonales del cuadrado-- vuelve a su posición inicial ¿Cuántos metros ha recorrido?