Problemas - Teoría de números
Clave secreta
Clave secreta
a) cinco cifras (dígitos)
b) el número es par
c)exactamente uno de los dígitos es impar
d)exactamente una de las cifras se repite, la que se repite es par y aparece en dos posiciones no consecutivas de la clave secreta
¿Cuántas claves (números de 5 cifras) son posibles bajo estas condiciones?
Dígitos finales, problema casi ateorico
Encontrar el entero positivo n más pequeño para el cual los últimos tres dígitos de 2007n (en la notación usual de base 10) son 837.
Sumar dígitos, problema ateórico
Un estudiante X forma un número entero escribiendo los números del 1 al 82 de manera ascendente, es decir, 1234567891011…808182. Encontrar la suma de los dígitos de este entero. R: 667
divisibilidad y division de polinomios
Encontrar todos los enteros positivos $ n $ distintos de la unidad para los cuales la expresión $(n^3-1)/(n^2+7n-8)$ es un entero.
El mulo y la burra generalizado (Problema 4, regiones 2008)
Abel le dice a Bárbara: si me dieras n yo tendría dos veces lo que a ti te quede. Bárbara le contesta: si tú me dieras 2 yo tendría n veces lo que a ti te quede. Encontrar todos los valores enteros positivos posibles de n.
ONMAS 2008 Nivel 1, Problema4
Francisco olvidó la clave de su tarjeta de banco y quiere realizar un retiro. Apenas recuerda que su clave contiene 4 dígitos y cumplen lo siguiente
- ninguno de los dígitos es 0 ni es mayor que 5
- no hay dígitos repetidos
- no hay dos dígitos adyacentes que sean números consecutivos
- la clave es un múltiplo de 4
Por ejemplo, el código 5413 no cumple porque el 4 y el 5 son cifras consecutivas, y el código 1135 no cumple porque se repite el 1. Francisco, que tiene muy mala suerte, probó todos los casos posibles y funcionó hasta que probó la última posibilidad. ¿Cuántos casos probó Francisco?
ONMAS 2008 Nivel 1, Problema 3
Juan tiene que llevar una ficha desde la esquina A hasta la esquina B, moviéndola por las líneas de la cuadrícula del tablero. La ficha puede moverse hacia arriba, hacia abajo, hacia la derecha o hacia la izquierda (la ficha puede pasar varias veces por el mismo punto). Cada vez que la ficha se mueve en sentido horizontal, Juan anota el número de la columna por la que atraviesa. Cuando la ficha finalmente llega a la esquina B, Juan multiplica todos los números que anotó. Encuentra todos los caminos donde el producto de los números anotados por Juan es 8640. Justifica tu respuesta.
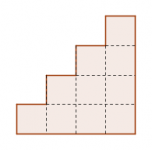
P4 OMM 2006. Zacatecas 2006: n-cubrimiento de una n-escalera
Como se sabe, en problemas de olimpiada, el enunciado puede tener una trampa de significado. El problema 4 del XX concurso nacional de la Olimpiada Mexicana de Matemáticas consiste de una pregunta “para qué enteros…”. La mayoría de los concursantes respondieron a la pregunta. Pero a la hora de las revisiones se supo que no bastaba con decir “estos son” sino que había que demostrar que no había otros. La solución necesitaba estar en el formato “los enteros n cumplen la condición si, y sólo si, son de la forma n = f(k)”. He aquí el enunciado del problema 4 del concurso nacional de 2006.
Un teorema sobre primos
Para todo primo $ p $, si $p^2 + 2$ es primo entonces $p^3 + 2$ es también primo.
Ternas Pitagóricas
Demuestre que para cualquier terna pitagórica $a^2+b^2=c^2$, alguno de los números $a, b, c$ es divisible por tres.
