Publicaciones Recientes
La preselección 2009
De este grupo se seleccionarán a los seis estudiantes que representarán a Tamaulipas en la Olimpiada Mexicana de Matemáticas 2009.
Problema 5 IMO 2005
Sea ABCD un cuadrilatero convexo con BC=DA y además las rectas BC,DA no son paralelas. Consideremos dos puntos variables E,F sobre BC,DA respectivamente, que satisfacen BE=DF . Sea P la interseccion de AC,BD. Las rectas BD y EF se intersectan en Q y las rectas AC y EF se intersectan en R.
Uno de Ciclicos (tema del 1er entrenamiento 09)
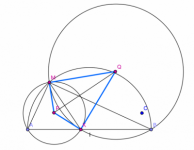
Sea AB diametro de una semicircunferencia. Un punto M sobre la semicircunferencia y K un punto spbre AB. Una circunferencia con centro P pasa por A,M,K, y otra circunferencia de centro Q pasa por M,K,B. Demostrar que MPKQ es un cuadrilatero ciclico.
PROBLEM 1 DE LA CENTRO
Determine el menor entero positivo N tal que la suma de sus dígitos sea 100 y la suma de 2N sea 110
Probar simediana
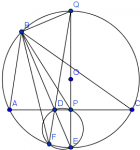
Considera un triangulo ABC Con BD su bisectriz interna ( D sobre AC) Sea E el punto donde se intersectan BD y el circuncirculo del triangulo ABC. El circulo de diametro DE corta al circuncirculo del triangulo ABC en los puntos D,F demuestra que BF es la simediana del triangulo ABC
Problema 2 BMO 2009
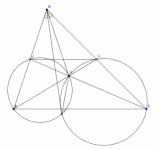
Sea MN una línea paralela al lado BC del triángulo ABC, con M sobre el lado AB y N sobre el lado AC. Las íineas BN y CM se intersectan en un punto P. Los circuncírculos de los triángulos BPM y CPN se intersectan en P y Q. Demostrar que ∠BAQ=∠CAP
Otro de un cuadrado, dentro de otro cuadrado.
Sea ABCD un cuadrado de centro O. Sean P, Q, R y S puntos en DA, AB, BC y CD, repectivamente, tales que P,O y R son colineales; y Q, O y S también lo son (colineales), y de manera que PR es perpendicular a QS. Demostrar que el cuadrilátero PQRS es un cuadrado.
L1.P23 (Un clásico --para terminar la lista)
Encontrar todas las soluciones en enteros positivos de la ecuación 1/x+1/y+1/z=1.
L1.P22 (Una ecuación cuadrática)
La ecuación x2+bx+2=0 tiene solamente una raíz. Determinar los valores de b.
L1.P21 (Cuadrado en el centro de un cuadrado)
Los puntos medios L,M,N,O de los lados QR,RS,SP,PQ de un cuadrado PQRS se unen con con un segmento de recta a los vértices de éste de manera que se forme un cuadrado P′Q′R′S′. Calcular la razón de áreas de los dos cuadrados.
