Publicaciones Recientes

Gracia por tu respuesta.

Sí, realmente es a la misma conclusion a la que yo he llegado porque resulta un triangulo rectangulo 3-4-5, despues de intentar multiples posibilidades, Mi duda realmente radica en que encontre el problema planteado en un texto clasico de geometria euclidiana (Elementos geometria plana por una reunion de profesores) en el cual no se usan las funciones trigonometricas para nada ( ni se mencionan) como debe serlo en esta área de la geometría.

Debido  a lo anterior se me ha ocurrido  y he intentado buscar relaciones entre algunas de las áreas en que se puede subdividir el problema, pero llego a un sitema de seis variables con cinco ecuaciones, que no me permite encontrar la relacion requerida.

El problema

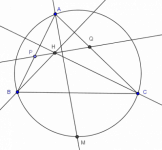
Sea $ABC$ un triángulo y sea $H$ su ortocentro. Sea $PQ$ un segmento que pasa por $H$ con $P$ en $AB$, $Q$ en $AC$ y tal que $\angle PHB=\angle CHQ$. Finalmente en el ciruncírculo del triángulo $ABC$ considera $M$ el punto medio del arco $BC$ que no contiene a $A$. Muestra que $MP=MQ$.

La solución

De acuerdo a los datos sobre la recta PQ que pasa por H, es fácil darse cuenta que PQ es bisectriz de los ángulos formados en H por las alturas.

Sea $I$ el incentro de un triángulo acutángulo $ABC$. La recta $AI$ corta por segunda vez al circuncírculo del triángulo $BIC$ en $E$. Sean $D$ el pie de la altura desde $A$ sobre $BC$ y $J$ la reflexión de $I$ con respecto a $BC$. Muestra que los puntos $D$, $J$ y $E$ son colineales.