Publicaciones Recientes
P3. OMM 1990. ¿Inducción? OK ¿Pero te queda claro qué debes demostrar?
Pruebe que $n^{n-1}-1$ es divisible entre $(n-1)^2$ para todo entero $n\geq2$
P2. OMM 1990. Relación de inradios
Sea $ABC$ un triángulo rectángulo con ángulo recto en $B$, y $H$ el punto de intersección del lado $AC$ y la altura por $B$. Llamemos $r,r_1,r_2$ a los radios de las circunferencias inscritas en los triángulos $ABC,ABH,HBC$, respectivamente. Encuentre una igualdad que relacione $r,r_1,r_2$.
P1. OMM 1990. Paseos en una cuadrícula
Encuentre el total de caminos que hay del punto $A$ a línea $l$ en la red de la siguiente figura, si en un camino solo está permitido ir hacia la izquierda.
Dispositivos: experimentales de Piaget y didácticos de Brousseau
Voy a elaborar en este post (en el sentido de decir más) sobre la diferencia entre interpretar las respuestas adolescentes ante una tarea de resolución de problemas -- en términos de sus posibles razonamientos y explicando sus errores según un esquema teórico-- y hacer lo mismo pero en una situación de enseñanza.
En particular, abundaré sobre la diferencia entre los dispositivos experimentales de Jean Piaget y las situaciones didácticas de Guy Brousseau. Usaré sendos ejemplos para que el lector pueda tener una comprensión inicial de la naturaleza de los dispositivos piagetianos, y las situaciones didácticas de Guy Brousseau.
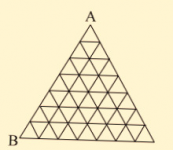
P6. OMM 1989. Trayectorias en retícula triangular
Siguiendo las líneas de la figura ¿Cuántos caminos hay para ir del punto $A$ al punto $B$ que no pasen dos veces por el mismo punto y que solo avancen hacia abajo y hacia los lados pero no hacia arriba?
P5. OMM 1989. Círculos tangentes
Sean $C_1$ y $C_2$ dos círculos tangentes de radio 1 dentro de un círculo $C$ de radio 2. Sea $C_3$ un círculo dentro de $C$ tangente a cada uno de los círculos $C,C_1,C_2$. Sea $C_4$ un círculo dentro de $C$ tangente a $C,C_1,C_3$. Demuestre que los centros de $C,C_1,C_3,C_4$ son los vértices de un rectángulo.
P4. OMM 1989. Números en expansión decimal
Encuentre el entero positivo mas pequeño $ n $ tal que, si su expansión decimal es $ n=a_ma_{m-1}\ldots{a_2}a_1a_0 $ y $r$ es el número cuya expansión decimal es $r=a_1a_0a_ma_{m-1}\ldots{a_2}0$, entonces $r$ es el doble de $n$.
P3. OMM 1989. Número de 1989 cifras
Pruebe que no existe un número positivo de 1989 cifras que tenga al menos tres de ellas iguales a 5 y tal que la suma de todas las cifras sea igual al producto de las mismas.
P2. OMM 1989. Múltiplos encadenados
Encuentre dos números enteros $a$ y $b$ tales que:
- $b^2$ es múltiplo de $a$;
- $a^3$ es múltiplo de $b^2$;
- $b^4$ es múltiplo de $a^3$;
- $a^5$ es múltiplo de $b^4$;
- pero $b^6$ no es múltiplo de $a^5$.
P1. OMM 1989. Áreas y medianas
Considere un triángulo $ABC$ en el que la longitud del lado $AB$ es 5, las medianas por $A$ y por $B$ son perpendiculares entre sí y el área es 18. Hallar las longitudes de los lados $BC$ y $AC$.
