Publicaciones Recientes
Selección Victoria de la OMM Tamaulipas 2011
El examen ciudades de la OMM tamaulipeca se realizó hoy en su versión Victoria en el COBAT 5. El examen consistió de 8 problemas, de los cuales solamente el octavo se puede considerar difícil. En total el examen valía 56 puntos. Los seleccionados Victoria son los siguientes.
Homotecia: de baricentros a puntos de Varignon
Las diagonales de un cuadrilátero convexo dividen a éste en cuatro triángulos. Demostrar que sus baricentros forman un paralelogramo.
Kafka en México --y la reforma 2011 en normales
En este post voy a comentar la reforma 2011 en normales, la cual aumenta a 5 años la duración de sus licenciaturas e incluye matemáticas como una de las materias a cursar. El evento es importante para la educación mexicana y atiende una recomendación de la OCDE del año pasado (mejorar la formación de sus profesores). Cito de mi post PISA, OCDE-recomendaciones y el efecto Casandra tal recomendación:
Convocatoria OMM 2011, Delegación Tamaulipas
Para todos los que estaban esperando la convocatoria de la Olimpiada Mexicana de Matemáticas en Tamaulipas, la pueden descargar del atachado --convertido a PDF, 1.8mb. El día 2 de septiembre es el concurso ciudades y el 9 el estatal. (Información proporcionada por el delegado Ramón J. Llanos Portales.)
Como dicen en Viento Libre: "tarde pero sin sueño" (En la OMM, Tamaulipas sólo puede mejorar... ¡ánimoooooooooo!)
Los saluda
jmd
Prototipos, ejemplos generales y categorización
Voy a elaborar en este post sobre un tema que atrajo mi atención hace algunos meses y que en estos días volví a estudiar. Es el tema de los prototipos --y su utilidad en la educación matemática.
¿Definir o no definir?
Si bien es cierto que las matemáticas escolares o, mejor dicho, la didáctica de las matemáticas escolares, rehuyen las definiciones, también lo es que en los cursos universitarios de matemáticas, y ciertamente en las matemáticas de concurso, las definiciones formales son imposibles de evitar (bueno, si es que realmente se quiere enseñar y aprender matemáticas y entrenar y ganar concursos).
El Cuadrado de Sócrates --y los triángulos notables
Voy a discutir en este post cuatro problemas de geometría básica que se resuelven de manera elemental invocando dos triángulos notables. Estos triángulos son el isósceles rectángulo (la mitad de un cuadrado) y el 30-60-90 (la mitad de un triángulo equilátero). En los dos problemas de inicio, la solución presentada invoca el isósceles rectángulo; en los otros dos se debe invocar la mitad de un equilátero.
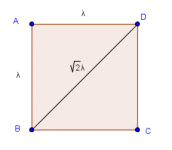
Primer problema (el Cuadrado de Sócrates)
Dado el lado $\lambda$ de un cuadrado, construir el cuadrado del doble de área.
Solución
Problema 3 (IMO 2011)
Sea $f$ una función del conjunto de los números reales en sí mismo que satisface $$f(x + y)\leq yf(x) + f(f(x))$$ para todo par de números reales $x, y$. Demostrar que $f(x) = 0$ para todo $x\leq0$.
Problema 2 (IMO 2011)
Sea $S$ un conjunto finito de dos o más puntos del plano. En $S$ no hay tres puntos colineales. Un remolino es un proceso que empieza con una recta $l$ que pasa por un único punto $P$ de $S$. Se rota $l$ en el sentido de las manecillas del reloj con centro en $P$ hasta que la recta encuentre por primera vez otro punto de $S$ al cual llamaremos $Q$. Con $Q$ como nuevo centro se sigue rotando la recta en el sentido de las manecillas del reloj hasta que la recta encuentre otro punto de $S$. Este proceso continúa indefinidamente.
Problema 1(IMO 2011)
Para cualquier conjunto de cuatro enteros positivos distintos se denota la suma con
Problema 6 (IMO 2011)
Sea $ABC$ un triángulo acutángulo con circuncírculo $\Gamma$. Sea $l$ una tangente a $\Gamma$, y sean $l_a,l_b,l_c$ las rectas obtenidas de $l$ mediante reflexión en $BC,CA,AB$, respectivamente. Demostrar que el circuncírculo del triángulo determinado por las rectas $l_a,l_b,l_c$ es tangente al círculo $\Gamma$.
