Publicaciones Recientes
36 Olimpiada Mexicana de Matemáticas en Tamaulipas
Con gusto anunciamos el inicio de la 36 Olimpiada Mexicana de Matemáticas en Tamaulipas.
Recuerda que si estás cursando primaria, secundaria o hasta 4to semestre de bachillerato, puedes inscribirte y participar.
Adjunto a este mensaje puedes encontrar la convocatoria completa, así como en el siguiente enlace: https://bit.ly/3tusl68
Además, en el siguiente formulario podrás realizar tu inscripción: https://forms.gle/vwrNBkwT5UrsguEKA
¡Mucho éxito!
Olimpiadas de Matemáticas de Nivel Básico 2022
Con mucho gusto damos inicio al Primer Examen de las Olimpiadas de Matemáticas en Tamaulipas en su categoría Educación Básica. Este comprende de 4to. grado escolar a 2do de secundaría. Podrás presentarlo a partir del viernes 6 de mayo y hasta el martes 10 mayo a las 10 pm. En el siguiente link, encontrarás el formulario de registro, el cual ya se encuentra abierto hasta el 10 de mayo. Al final del registro encontrarás el link al examen, que de igual manera se publicará por los medios difusión autorizados y se enviaran vía correo a los registrados.
La desigualdad más simple
Una preguntar muy común en matemáticas de concurso y escolares es la siguiente:
¿Cuál es el área rectangular más grande que se puede cubrir con un cerca de 500 metros de longitud?
Probablemente esté más comúnmente en cursos de precálculo o de de calculo diferencial I. Pero también puede aparecer en cursos de álgebra. La técnica que veremos aquí, es para aquellos que quieren resolverlo usando sólo álgebra (con muy poco conocimiento de desigualdades).
Las técnica podría presentarse a estudiantes de secundaria interesados en Matemáticas de Concurso. Pues es fácil de presentar si ya saben álgebra.
Subconjuntos con promedio entero
Secuencia de conjuntos no vacios (OMM 2021 P6)
Determina todos los conjuntos no vacíos C1,C2,C3,…, tales que cada uno de ellos tiene un número finito de elementos y todos sus elementos son enteros positivos, con la siguiente propiedad: Para cualesquiera enteros positivos m y n, la cantidad de enteros positivos en el conjunto Cm más la cantidad de enteros positivos en Cn es igual a la suma de los elementos en el conjunto Cm+n.
Nota: Al denotar con |Ck| la cantidad de elementos de Ck y con Sk la suma de los elementos de Ck, la condición del problema es que para m , n enteros positivos se cumple
|Cn|+|Cm|=Sm+nNúmeros digitales (OMM 2021 P5)
Para cada entero n>0 con expansión decimal ¯a1a2…ak definimos s(n) como sigue:
- Si k es par, s(n)=¯a1a2+¯a3a4+⋯+¯ak−1ak
- Si k es impar, s(n)=a1+¯a2a3+¯a4a5+⋯+¯ak−1ak
Por ejemplo, si n=123 entonces s(n)=1+23=24 y si n=2021 entonces s(n)=20+21=41.
Decimos que este n es digital si n es múltiplo de s(n). Muestra que entre cualesquiera 198 enteros positivos consecutivos, todos ellos menores que 2000021, hay uno de ellos que es digital.
Triángulo con ángulo de 60º (OMM 2021 P4)
Sea ABC un triángulo acutángulo escaleno con ∠BAC=60∘ y ortocentro H. Sea ωb la circunferencia que pasa por H y es tangente a AB en B, y ωc la circunferencia que pasa por H y es tangente a AC en C.
- Prueba que ωb y ωc solamente tienen a H como punto común
- Prueba que la recta que pasa por H y el ortocentro O de ABC es tangente común a ωb y ωc
Criterio del 99 (P5 OMM 2021)
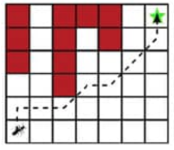
La hormiga, el mago y la lava (OMM 2021 P3)
Sean m,n≥2 dos enteros. En una cuadrícula de m×n, una hormiga empieza en cuadrito inferior izquierdo y quiere camina al cuadradito superior derecho. Cada paso que da la hormiga debe ser a un cuadrito adyacente, de acuerdo a las siguientes posibilidades ↑, → y ↗. Sin embargo, un malvado mago ha dejado caer lava desde arriba y ha destruido algunos cuadritos de forma tal que:
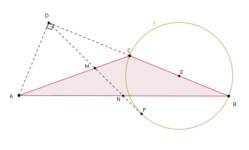
Es punto medio si y sólo si el otro es punto medio (OMM 2021 P2)
Sea ABC un triángulo tal que ∠ACB>90∘ y sea D el punto de la recta BC tal que AD es perpendicular a BC. Considere Γ la circunferencia de diámetro BC. Una recta que pasa por D es tangente a la circunferencia Γ en P, corta al lado AC en M (quedando M entre A y C) y corta al lado AB en N.
Demuestra que M es punto medio de DP si, y sólo si N es punto medio de AB.