Publicaciones Recientes
Mayor divisor, 7 veces el menor
Encontrar todos los números naturales n tales que sus divisores, distintos de 1 y n, cumplen que el más grande es 7 veces el más pequeño.
Altura de un paralelogramo
En la figura, el rectángulo tiene lados de 10 cm. y de 8 cm. y éstos se han dividido como se indica de manera que al unir los puntos de división se forma un paralelogramo (ojo sus ángulos no son rectos). Calcula la distancia entre los lados paralelos más pequeños, indicada con la línea d.
Cuadrados perfectos de tres dígitos consecutivos
Encuentra todos los números de tres cifras que sean cuadrados perfectos y que use cifras consecutivas. Por ejemplo 123, 132, 213, 231,312, 321 son números que usan las cifras consecutivas y 4 es un ejemplo de cuadrado perfecto.
El odómetro chafa
El odómetro (medidor de distancias recorridas) de un carro chafa siempre brinca de 3 a 5, saltándose el 4, sin importar la posición. Por ejemplo, después de viajar un kilómetro cambió de 000039 a 000050. Si el odómetro marca 002005, ¿cuántos kilómetros ha viajado en realidad el carro chafa?
Fichas en progresión aritmética
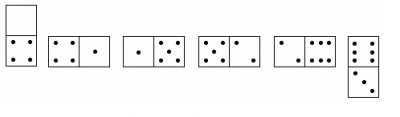
Como se ve en la ilustración se han jugado seis fichas de dominó. De acuerdo a las reglas del juego, se une 4 con 4, 1 con 1, y así sucesivamente. Para el caso de la figura, la suma de los puntos de cada ficha son 4, 5, 6, 7, 8, 9 y están en progresión aritmética, es decir, los números tomados en orden tienen una diferencia común, en este caso particular el 1.
¿De cuántos modos podemos jugar seis fichas de dominó, tomadas de una caja común de veintiocho, para que los números queden en progresión aritmética?
Años superolímpicos
Cuando la edición N de la ONMAS se realiza en un año divisible entre N, diremos que es un año superolímpico. Por ejemplo el año 2005 es superolímpico porque se realiza la edición 5 de la ONMAS y 2005 es divisible entre 5. Determina todos los años superolímpicos, sabiendo que la ONMAS se realiza anualmente a partir de 2001 y suponiendo que se seguirá realizando cada año.
Triángulos en una circunferencia
Sean AB es el diámetro de una circunferencia con centro en el punto D, y C un punto en AB de tal manera que AC es la mitad de CB. Por el punto C se traza una perpendicular a AB que corta a la circunferencia en los puntos E y F. Si el área del triángulo ABE es de 60cm2 ¿cuánto vale el área del triángulo DEF?
EGMO Problema 2 - Máxima cantidad de renglones en una tabla
Sea n un entero positivo, encuentra el entero más grande m, en términos de n con la siguiente propiedad:
Una tabla con m renglones y n columnas puede ser llenada con números reales de tal manera que dos diferentes renglones, [a1,a2,…,an] and [b1,b2,…,bn] satisfacen que max(|a1−b1|,|a2−b2|,…,|an−bn|)=1.
©Traducido de la versión en ingles por Matetam.com
EGMO Problema 1 - Sobre dos circuncentros y demostrar que una línea es perpendicular
Sea ABC un triángulo con circuncentro O. Los puntos D, E y F se encuntran en el interio de los lados BC, CA y AB respectivamente, de tal manera que DE es perpendicular a CO y DF such that DE is perpendicular to CO and DF is perpendicular to BO. (Por punto interior nos referimos, por ejemplo, a que el punto D se encuentra sobre la línea BC y D está entre B y C en esa línea)
Consideremos K el circuncentro del triángulo AFE. Desmuestra que las líneas DK y BC son perpendiculares.
©Traducido de la versión en ingles para Matetam.com
Kevin: talento matemático infantil --en la periferia
Hablando de la educación matemática en USA, un matemático americano desencantado decía: lo verdaderamente extraordinario es encontrar un niño que resuelva problemas de rutina con métodos de rutina. (Ver la segunda postdata de mi post sobre la división larga.)
Hay pocas cosas que le alegran el día a un profesor de matemáticas desencantado de la educación. Una de ellas es encontrar o descubrir un niño con aquellas habilidades matemáticas que solían ser las obligatorias.