Publicaciones Recientes
Condición necesaria para cuadrado mágico
Demostrar que en el cuadrado mágico normal 3×3, el 5 va en el centro. (Es decir, el 5 en el centro es condición necesaria para que se forme cuadrado mágico.)
Cálculo de la constante mágica
Se le llama suma mágica o constante mágica a la suma de una fila, una columna o una diagonal principal de un cuadrado mágico normal n\timesn. (Se le llama cuadrado mágico normal a un cuadrado mágico que usa los números del 1 al n2.)
- Demostrar que la suma mágica es s=n(n2+1)/2
- Demostrar que la suma mágica puede ser calculada colocando los números del 1 al n2 en el orden natural por filas (los primeros n en la primera fila, del n+1 a 2n en la segunda, etc.) y calculando la suma de cualquier diagonal principal.
Suma (o constante) mágica
Demostrar que al colocar los números del 1 al n2 en una matriz n×n en el orden natural por filas (los primeros n en la primera fila, del n+1 a 2n en la segunda, etc.) la suma de los números en cualquier diagonal principal es la misma y es s=n(n2+1)/2. Por ejemplo en
Sobre la teoría de reificación de Anna Sfard
Trigonometría en el examen ENLACE 2010
Cuadrilátero completo y puntos medios de sus diagonales
Consideremos a, b, c y d cuatro rectas no tres de ellas concurrentes (es decir, un cuadrilátero completo) y no dos de ellas paralelas. Demuestra que son colineales los puntos medios de las tres diagonales del cuadrilátero completo.
Nota: Las diagonales de un cuadrilátero completo son los segmentos que unen un punto de intersección de dos de sus lados con el de los otros dos lados.
Comentarios finales
Se puede deducir el criterio LLL a partir del LAL aplicando las propiedades del triángulo isósceles: los triángulos en correspondencia LAL se colocan como se muestra en la figura y…
Puesto que AB=IJ y AB=IK, tenemos los isósceles ABI y ACI. Pero entonces sus ángulos en la base son iguales.
Sumando, se obtiene que los ángulos en A y en I son iguales y estamos ya en posibilidad de aplicar el criterio LAL para asegurar que los triángulos ABC e IJK son congruentes.
Un teorema de medianas
La demostración del siguiente teorema es instructiva de cómo un trazo auxiliar permite el uso de resultados elementales (en este caso congruencia de triángulos) en la solución de problemas geométricos.
Pero también nos enseña el razonamiento en reversa, muy útil en la demostración de teoremas geométricos del tipo “si y sólo si.” No está de más añadir que lo más instructivo de las demostraciones de los teoremas elementales de geometría es la construcción de las figuras.
Segundo teorema de la línea media
La paralela a la base que pasa por el punto medio de un lado pasa también por el punto medio del otro lado.
Demostración:
Otra vez el trazo auxiliar que ayuda a la demostración es clásico y muy instructivo. Sea ABC el triángulo y N el punto medio de AC. Por N tracemos una paralela NM a la base BC. Vamos a demostrar que M es punto medio de AC.
El trazo auxiliar consiste en el segmento que une N con el punto medio K de la base BC. Este trazo nos permite aplicar el primer teorema de la línea media y asegurar KN//AB y KN=AB/2. Pero entonces:
Primer teorema de la línea media
La línea media de un triángulo es paralela a la base y mide la mitad de ésta.
Demostración:
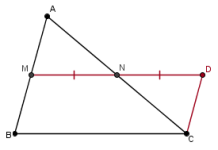
Tracemos la línea media MN de los lados AB y AC del triángulo ABC. El trazo auxiliar que necesitamos es prolongar MN hasta D de tal manera que MN=ND. (Nota: la demostración es clásica y es instructiva de cómo usar trazos auxiliares en la solución de problemas geométricos.)
Los triángulos MNA y DNC son congruentes (criterio LAL).