Publicaciones Recientes
Una recta variable que pasa por un punto fijo
El punto P está fijo en una circunferencia y el punto Q está fijo en una recta. Un punto variable R se mueve sobre la circunferencia pero sin alinearse con P y Q. La circunferencia por P,Q y R corta a la recta de nuevo en V. Demostrar que la recta VR pasa por un punto fijo.
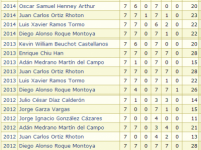
Resultados del primer selectivo OMM_Tam_2014
A continuación se presentan los resultados del primer selectivo OMM Tamaulipas 2014. ¡Ánimoooo!
Primos y divisibilidad: dos problemas
Voy a comentar en este post las soluciones de los problemas 1 y 2 del primer selectivo para la preselección OMM Tamaulipas 2014. Espero que sirva como feedback para los preseleccionados que no los resolvieron o los resolvieron de otra forma. (Vaya una felicitación para Camilo por su excelente elección de los problemas.)
Problema 1. Sean m,n enteros positivos tales que $m^2+n^2$ es múltiplo de 3. Pruebe que m y n son también múltiplos de 3.
Comentario:
Examen selectivo 1, OMM_Tam_2014
El fin de semana (8,9 y 10 de agosto) se llevó a cabo el primer entrenamiento de la preselección OMM Tamaulipas 2014 y se realizó el primer examen selectivo, el cual reproduzco a continuación.
El entrenamiento estuvo a cargo de Luis Camilo Castillo Toledano (las gracias le sean dadas) y el tema fue teoría de números.
Problema 1. Sean $m,n$ enteros positivos tales que $m^2+n^2$ es múltiplo de 3. Pruebe que $m$ y $n$ son también múltiplos de 3.
Problema 2. Encontrar todos los números primos $p,q$ tales que su suma y su diferencia también son números primos.
Líneas isogonales y circunferencias con centro en los lados.
Sea $ABCD$ un cuadrilátero cíclico convexo. Sea $H$ un punto sobre $BD$ tal que $AH$ y $AC$ son líneas isogonales (reflejadas en la bisectriz del ángulo en $A$).
Consideremos $\mathcal{C}_B$ y $\mathcal{C}_D$ las circunferencias con cuerda $HC$ y con sus respectivos centros en $AB$ y $AD$.
Llamemos $S$ y $P$ a la intersección de $\mathcal{C}_B$ con la recta $AB$; el vértice $A$ más cerca de $S$ que de $P$. Análogamente llamemos $T$ y $Q$ a la intersección de $\mathcal{C}_D$ con la recta $AD$; el vértice $A$ más cerca de $T$ que de $Q$. Entonces se satisfacen las siguiente propiedades
México en la IMO 2014 --y la agenda oculta de Diego
Puede que sea ya muy tarde pero este post lo voy a dedicar a la participación de México en la IMO 2014 --y a Diego. (Como se sabe la Olimpiada Internacional de Matemáticas se llevó a cabo la semana del 3 al 13 de julio, en Cape Town, Sudáfrica.)
Una de las cosas que llama la atención de las estadísticas (ver Sitio Oficial de la IMO) es que la selección mexicana prácticamente no le dedica tiempo a los difíciles (el 3 y el 6) y que los dos oros que hemos logrado son de 28 puntos.
P6. IMO 2014 - Coloreado de rectas en posición general
Un conjunto de rectas en el plano está en posición general si no hay dos que sean paralelas ni tres que pasen por el mismo punto. Un conjunto de rectas en posición general separa el plano en regiones, algunas de las cuales tienen área finita; a estas las llamamos sus regiones finitas.
Demostrar que para cada $n$ suficientemente grande, en cualquier conjunto de $n$ rectas en posición general es posible colorear de azul al menos $\sqrt{n}$ de ellas de tal manera que ninguna de sus regiones finitas tenga todos los lados de su frontera azules.
P5. IMO 2014 - Monedas fraccionarias
Para cada entero positivo $n$, el Banco de Ciudad del Cabo produce monedas de valor $\frac{1}{n}$. Dada una colección finita de tales monedas (no necesariamente de distintos valores) cuyo valor total no supera $99 + \frac{1}{2}$, demostrar que es posible separar esta colección en 100 o menos montones, de modo que el valor total de cada montón sea como máximo 1.
P4. IMO 2014 - Concurrencia de dos rectas y una circunferencia
Los puntos $P$ y $Q$ están en el lado $BC$ del triángulo acutángulo $ABC$ de modo que $\angle PAB = \angle BCA$ y $\angle CAQ = \angle ABC$. Los puntos $M$ y $N$ están en las rectas $AP$ y $AQ$, respectivamente, de modo que $P$ es el punto medio de $AM$, y $Q$ es el punto medio de $AN$. Demostrar que las rectas $BM$ y $CN$ se cortan en la circunferencia circunscrita del triángulo $ABC$
P3. IMO 2014 - Demuestra que es tangente
En el cuadrilátero convexo $ABCD$, se tiene $\angle ABC = \angle CDA = 90^{\circ}$. La perpendicular a $BD$ desde $A$ corta a $BD$ en el punto $H$. Los puntos $S$ y $T$ están en los lados $AB$ y $AD$, respectivamente, y son tales que $H$ está dentro del triángulo $SCT$ y
$$\angle CHS - \angle CSB = 90^{\circ},\quad \angle THC - \angle DTC = 90^{\circ}$$.
Demostrar que la recta $BD$ es tangente a la circunferencia circunscrita del triángulo $TSH$.
