Combinatoria
P2 OMM 1992. Cuartetas y múltiplos de un primo
Sea p un número primo, diga cuántas cuartetas distintas (a,b,c,d) existen, con a, b, c y d enteros y 0≤a,b,c,d≤p−1, tales que ad−bc sea múltiplo de p.
P1. OMM 1990. Paseos en una cuadrícula
Encuentre el total de caminos que hay del punto A a línea l en la red de la siguiente figura, si en un camino solo está permitido ir hacia la izquierda.
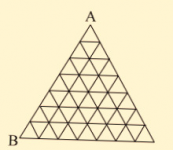
P6. OMM 1989. Trayectorias en retícula triangular
Siguiendo las líneas de la figura ¿Cuántos caminos hay para ir del punto A al punto B que no pasen dos veces por el mismo punto y que solo avancen hacia abajo y hacia los lados pero no hacia arriba?
P7. OMM 1988. Subconjuntos ajenos de {1,2,...,m}
Si A y B son subconjuntos ajenos del conjunto {1,2,…,m} y la suma de los elementos de A es igual a la suma de los elementos de B, pruebe que el número de elementos de A y también de B es menor que m/√2
P4. OMM 1988. Ocho enteros entre uno y ocho
¿Cuántas maneras hay de escoger ocho enteros a1,a2,a3,…,a8 no necesariamente distintos, tales que 1≤a1≤…≤a8≤8?
Embaldosado de un patio
Se desea embaldosar un patio cuadrado de lado N entero positivo. Se dispone de dos tipos de baldosas: cuadradas de 5×5, y rectangulares de 1×3. Determine los valores de N para los cuales es posible hacerlo. Nota: el patio debe quedar completamente cubierto sin que las baldosas se sobrepongan.
Mover una ficha en un tablero
Un jugador coloca una ficha en una casilla de un tablero m\timesn dividido en cuadrados de tamaño 1×1. El jugador mueve la ficha de acuerdo a las siguientes reglas:
- En cada movida, el jugador mueve la ficha a un cuadrado que comparte un lado con el cuadrado en que se encuentra.
- El jugador no puede mover la ficha a un cuadrado que ha ocupado previamente.
- Dos movimientos consecutivos no pueden tener la misma dirección.
El juego termina cuando el jugador no puede mover la ficha. Determine todos los valores de m y n tales que, al colocar la ficha en algún cuadrado, todos los cuadrados pueden ser ocupados durante el juego.
No podrían saludar sólo a uno
Cada uno de los 61 competidores en el concurso estatal saludó de mano al menos a otro competidor. Demostrar que alguno de ellos saludó de mano al menos a dos competidores.
Problema 2
Sea S el conjunto de puntos (i,j) de coordenadas enteras en el plano, con i,j=0,1,2,...,9.
Coloración de vertices
Demuestra que una gráfica G es bipartita si y sólo si su número cromático χ(G) es 2.
