Publicaciones Recientes
Problema técnico de primos
Encuentra la suma de los números primos que dividen a todos los números de 3 dígitos con todos ellos iguales.
Torneo de Ping Pong
En una escuela hubo un torneo de Ping Pong. La escuela cuenta con 2 mesas para jugar y en total hubo 6 partidos. Los partidos duraron 8, 10, 12, 17, 21 y 22 minutos y es posible comenzar un partido justo al terminar el anterior. Si el torneo comenzó a las 9:00 de la mañana, ¿a qué hora es lo más temprano que pudo terminar el torneo?
Los favoritos de Claudia
Claudia escribe una lista de sus 11 números favoritos más pequeños. El primero es el 5 y el tercero es 13, además, se dió cuenta que todos los números excepto el primero y el último resultan ser el promedio de los dos números que tiene a lado. ¿Cuál es el último número de su lista?
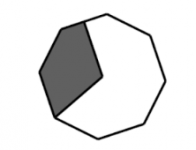
Uno imposible de un octágono
El área total del siguiente octágono es de 2022 cm2, ¿cuál es el área de la región sombreada?
Multiplica las fechas
En una fecha escrita de la forma aa/mm/yy o a/m/yy se multiplican los digitos usados para escribirlas, por ejemplo 24/12/22 da 2x4x1x2x2x2=64 o 5/8/22 da 5x8x2x2=160. ¿Cuántas fechas de la década de los 2020's cumplen que la multiplicación de los dígitos da 120?
Suelo con mosaicos
Un suelo se va a llenar con mosaicos como el siguiente, formado por mosaicos cafés más pequeños como los mostrados en la figura. El área blanca se llenará con mosaicos azules del mismo tamaño que el café. Al llenarse todo el suelo se utilizaron 192 cafés, ¿cuántos mosaicos azules fueron necesarios?

Piezas rectangulares con área 240
Se van a construir piezas rectangulares de área 240 cm2 y con ambos lados entero. ¿De cuántas formas distintas se puede hacer?
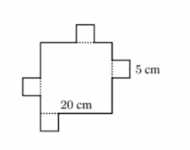
Halla el perímetro
Sobre los lados de un cuadrado de 20 x 20 cm se dibujan cuadrados de 5 x 5 cm como se muestra en la figura. ¿Cuál es el perímetro de la siguiente figura?
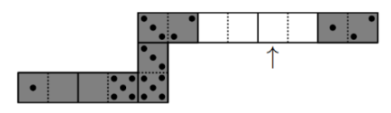
Fichas de dominó
Pancho hizo una hilera con 7 fichas de dominó de manera que los lados con el mismo número de puntos quedaron uno al lado del otro. Originalmente la hilera tenía un total de 33 puntos, pero el hermanito de Pancho se llevó dos de las fichas. ¿Qué cantidad de puntos había en el lugar que señala la flecha en la figura?
P3 IMO 1993 - Tablero de ajedrez infinito
Sobre un tablero de ajedrez infinito se juega de la siguiente manera:
Al principio hay $n^2$ fichas dispuestas sobre el tablero en un cuadrado de $n\times n$ de casillas adyacentes, con una ficha en cada casilla. Cada jugada es un salto de una ficha en dirección horizontal o vertical sobre una casilla adyacente, ocupada por otra, hasta una no ocupada, contigua a ella. La ficha sobre la que se ha saltado se retira. Halle los valores de $n$ para los que el juego puede terminar quedando una única ficha en el tablero.
