Publicaciones Recientes
Calculo de area
Es posible calcular el área sombreada solo en funcion de R(no deben aparecer mas variables, como por ejemplo ángulos), por medio de relaciones geométricas, sin usar las funciones trigonométricas, ni integracion.
Sobre el problema 1 de la 29 OMM
El problema
Sea ABC un triángulo y sea H su ortocentro. Sea PQ un segmento que pasa por H con P en AB, Q en AC y tal que ∠PHB=∠CHQ. Finalmente en el ciruncírculo del triángulo ABC considera M el punto medio del arco BC que no contiene a A. Muestra que MP=MQ.
La solución
De acuerdo a los datos sobre la recta PQ que pasa por H, es fácil darse cuenta que PQ es bisectriz de los ángulos formados en H por las alturas.
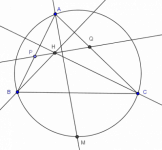
Problema 6. 29a Olimpiada Mexicana de Matemáticas
Problema 5. 29a Olimpiada Mexicana de Matemáticas
Sea I el incentro de un triángulo acutángulo ABC. La recta AI corta por segunda vez al circuncírculo del triángulo BIC en E. Sean D el pie de la altura desde A sobre BC y J la reflexión de I con respecto a BC. Muestra que los puntos D, J y E son colineales.
Problema 4. 29a Olimpiada Mexicana de Matemáticas
Problema 3. 29a Olimpiada Mexicana de Matemáticas
- f(1)=1
- Para todos a,b enteros positivos, se cumple que
f(a+b+ab)=a+b+f(ab) .
Problema 2. 29a Olimpiada Mexicana de Matemáticas
Sean n un entero positivo y k un entero entre 1 y n. Se tiene un tablero de n×n color blanco. Se hace el siguiente proceso. Se dibujan k rectángulos con lados de longitud entera, con lados paralelos a los del tablero y tales que su esquina superior derecha coincide con la del tablero. Luego, estos k rectángulos se rellenan de negro. Esto deja una figura blanca en el tablero. ¿Cuántas figuras blancas diferentes podemos obtener, que no se puedan obtener haciendo el proceso con menos de k rectángulos?
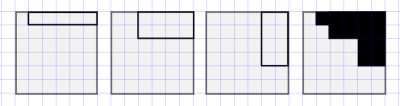
Problema 1. 29a Olimpiada Mexicana de Matemáticas
Sea ABC un triángulo y sea H su ortocentro. Sea PQ un segmento que pasa por H con P en AB, Q en AC y tal que ∠PHB=∠CHQ. Finalmente en el ciruncírculo del triángulo ABC considera M el punto medio del arco BC que no contiene a A. Muestra que MP=MQ.
Selección Tamaulipas 2015 y un examen muy difícil.
Preselección Tamaulipas OMM 2015
Enseguida se enlistan los 16 preseleccionados que se mantienen en la competencia para elegir la selección Tamaulipas OMM 2015.
Nombre Escuela Ciudad Puntaje
