Publicaciones Recientes
Problema 5. 29a Olimpiada Mexicana de Matemáticas
Sea $I$ el incentro de un triángulo acutángulo $ABC$. La recta $AI$ corta por segunda vez al circuncírculo del triángulo $BIC$ en $E$. Sean $D$ el pie de la altura desde $A$ sobre $BC$ y $J$ la reflexión de $I$ con respecto a $BC$. Muestra que los puntos $D$, $J$ y $E$ son colineales.
Problema 4. 29a Olimpiada Mexicana de Matemáticas
Problema 3. 29a Olimpiada Mexicana de Matemáticas
- $f(1)=1$
- Para todos $a,b$ enteros positivos, se cumple que
$$f(a+b+ab)=a+b+f(ab)$$ .
Problema 2. 29a Olimpiada Mexicana de Matemáticas
Sean $n$ un entero positivo y $k$ un entero entre $1$ y $n$. Se tiene un tablero de $n \times n$ color blanco. Se hace el siguiente proceso. Se dibujan $k$ rectángulos con lados de longitud entera, con lados paralelos a los del tablero y tales que su esquina superior derecha coincide con la del tablero. Luego, estos $k$ rectángulos se rellenan de negro. Esto deja una figura blanca en el tablero. ¿Cuántas figuras blancas diferentes podemos obtener, que no se puedan obtener haciendo el proceso con menos de $k$ rectángulos?
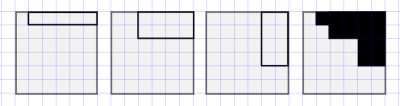
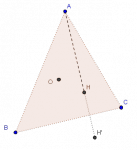
Problema 1. 29a Olimpiada Mexicana de Matemáticas
Sea $ABC$ un triángulo y sea $H$ su ortocentro. Sea $PQ$ un segmento que pasa por $H$ con $P$ en $AB$, $Q$ en $AC$ y tal que $\angle PHB=\angle CHQ$. Finalmente en el ciruncírculo del triángulo $ABC$ considera $M$ el punto medio del arco $BC$ que no contiene a $A$. Muestra que $MP=MQ$.
Selección Tamaulipas 2015 y un examen muy difícil.
Preselección Tamaulipas OMM 2015
Enseguida se enlistan los 16 preseleccionados que se mantienen en la competencia para elegir la selección Tamaulipas OMM 2015.
Nombre Escuela Ciudad Puntaje
La dificultad de un problema depende del resolutor
En el presente post voy a presentar la solución de un problema de números que se me hizo realmente difícil y no lo pude resolver sin ayuda. Trato también de trasmitir a los lectores de MaTeTaM el modo de razonar de un experto en el problem solving de concurso. El problema es el siguiente:
Demostrar que, para todo entero no negativo k, $$2^{2^{6k+2}}+3$$ es múltiplo de 19.
Demostración (reconstruida a partir de una realizada por JRV en conversación telefónica con el que esto escribe)

Sobre el ortocentro reflejado y el problema 3G
Creo que puede ser de alguna utilidad para los lectores de MaTeTaM la discusión de dos demostraciones del conocido teorema que dice:
El reflejo del ortocentro en el espejo de cualquier lado del triángulo pertenece al circuncírculo.
Una de ellas procede reflejando $H$ en un lado (digamos $BC$) y demuestra que ese reflejo (digamos $H'$) pertenece al circuncírculo; la otra toma el punto $H'$ de intersección de la altura (digamos $AH$) con el circuncírculo y demuestra que $H'$ es el reflejo de $H$ (en $BC$).
Resultados del concurso estatal Tamaulipas 2015
El concurso estatal de la Olimpiada Mexicana de Matemáticas Tamaulipas 2015 se celebró el viernes 28 de agosto en las instalaciones de la UAMCEH-UAT en Cd Victoria. Fueron 4 problemas de diversa dificultad los cuales se pueden ver en la sección de problemas de este sitio web.
El problema 1(A) fue el regalo para que nadie se sintiera mal. Pero a los participantes se les hizo muy difícil (según se puede ver por el número de ceros que recibió).
