Filosóficos
Principio de cooperación
Nietzsche, el nihilismo --y la reducción al absurdo
El último jueves del mes pasado ofrecí una charla sobre Nietzsche en la UAMCEH_UAT dentro del seminario de filosofía denominado Café y Rollos. Atacho el texto en que basé la presentación. Está en forma de cuadernillo, es decir, hay que imprimir a doble cara y después doblar a la mitad.
La parte de la charla que podría ser de interés para los lectores de MaTeTaM es la que presento en este post. Presenta el método de prueba de la reducción al absurdo con un trasfondo nihilista. Me sirvió para mostrar el lado no negativo de Nietzsche y el Nihilismo.
Sobre el concepto de frónesis en el problem solving
Estructura de los problemas de variación inversa
En este post voy a presentar la cuestión de que si el alumno no cumple los pre-requisitos para estar en un cierto nivel escolar, entonces la educación se convierte en una farsa. Porque, siendo realistas, el profesor no tomará medidas remediales para sus alumnos más débiles. En primer lugar porque el tiempo del aula es un recurso escaso. En segundo lugar porque interpretará los excesivamente laxos filtros de entrada de la administración escolar como un insulto a su profesión. (Un primer pre-requisito es ¿sabe leer? --¿es esto mucho pedir?).
Kafka en México --y la reforma 2011 en normales
En este post voy a comentar la reforma 2011 en normales, la cual aumenta a 5 años la duración de sus licenciaturas e incluye matemáticas como una de las materias a cursar. El evento es importante para la educación mexicana y atiende una recomendación de la OCDE del año pasado (mejorar la formación de sus profesores). Cito de mi post PISA, OCDE-recomendaciones y el efecto Casandra tal recomendación:
Prototipos, ejemplos generales y categorización
Voy a elaborar en este post sobre un tema que atrajo mi atención hace algunos meses y que en estos días volví a estudiar. Es el tema de los prototipos --y su utilidad en la educación matemática.
¿Definir o no definir?
Si bien es cierto que las matemáticas escolares o, mejor dicho, la didáctica de las matemáticas escolares, rehuyen las definiciones, también lo es que en los cursos universitarios de matemáticas, y ciertamente en las matemáticas de concurso, las definiciones formales son imposibles de evitar (bueno, si es que realmente se quiere enseñar y aprender matemáticas y entrenar y ganar concursos).
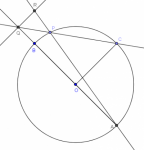
Una comunicación que calla: sobre el concepto de antiparalelas
Voy a ilustrar en este post la multiplicidad de conexiones que un cognizador debería establecer con una teoría previa en el momento de resolver (o estudiar la solución a) un problema de matemáticas escolares. Sostengo que la forma condensada de presentar las soluciones es una forma reticente de comunicar --así sea de manera involuntaria o por razones de estilo de redacción.
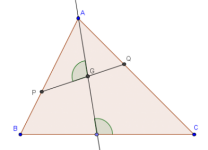
El cuadrado de Polya --con Geogebra
En este post comento sobre un posible proceso de solución al problema clásico de inscribir un cuadrado en un triángulo, usando el software de geometría dinamico Geogebra.
El cuadrado de Polya
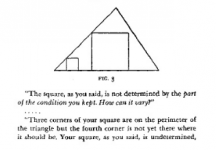
En el problem solving de las matemáticas escolares hay algunos problemas que son ya legendarios. Uno de ellos es el problema del cuadrado de Polya. Se trata de inscribir un cuadrado en un triángulo. A continuación su enunciado:
Inscribir un cuadrado en un triángulo $ABC$. Dos de los vértices del cuadrado deben estar en la base $BC$, y los otros dos en los otros dos lados, uno en cada uno.
Ficciones matemáticas
El aspecto visual de las matemáticas y la conceptualización
