Intermedio
Dos homotecias en un trapecio
Las prolongaciones de los lados AB y CD de un trapecio se intersecan en K, y sus diagonales en L. Si M,N son los puntos medios de de las bases, demostrar que los puntos K,L,M,N están en una misma recta.
Paralelogramo de baricentros
Las diagonales de un cuadrilátero convexo dividen a éste en cuatro triángulos. Demostrar que sus baricentros forman un paralelogramo.
Transformación geométrica de una circunferencia
Sean dadas dos circunferencias de radios diferentes y una afuera de la otra, y H la intersección de sus tangentes exteriores comunes. Demostrar que para cualquier punto A en una de las circunferencias, existe un punto B en la otra de tal manera que HA⋅HB=HP⋅HQ, donde P,Q son los puntos de tangencia de una de las tangentes comunes.
Transformación geométrica de una recta
Sean dadas una circunferencia de radio r y centro O, y una recta l. Encontrar el lugar geométrico de los puntos Y tales que OX⋅OY=r2, cuando X se mueve sobre l.
Transformación geométrica de un punto
Sean dados una circunferencia de centro O y radio r, y un punto A en su interior distinto de O. Encontrar un punto B en el plano de tal manera que OA⋅OB=r2. Justifica tu respuesta demostrando la validez del procedimiento que ubica el punto B.
Antiparalelas
Dos rectas se dicen antiparalelas, respecto a un ángulo de referencia, si forman el mismo ángulo en lados opuestos de la bisectriz de ese ángulo.
Demostrar que:
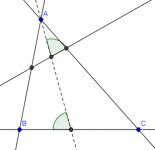
La clave está en la figura
En el triángulo ABC, rectángulo en C, la bisectriz de A corta a BC en P y la bisectriz de B corta a CA en Q. Sean M y N las proyecciones de P y Q, respectivamente, sobre el lado AB . Calcular la medida del ángulo MCN.
Una propiedad banal de dos isogonales
Sea ABC un triángulo y Γ su circuncírculo con centro O. La altura de A y el radio OA forman un ángulo cuya medida es la diferencia de las de B y C
Reflejos en el espejo de la bisectiz
Dentro del triángulo ABC, considere un punto P, y C′ y B′, los pies de las perpendiculares bajadas desde P a los lados AB y AC, respectivamente. Demostrar que si Q es un punto tal que C′PB′Q es paralelogramo, entonces las rectas AP y AQ son simétricas respecto a la bisectriz del ángulo A.
Sucesión de cuadrados
Demostrar que todos los números de la siguiente sucesión son cuadrados perfectos: 49, 4489,444889,...
