Intermedio

Determina si existen infinitos enteros $ k $, que cumplen que para cualquier primo $ p $, el numero $p^2+k$ siempre es compuesto.

Por ejemplo si tomamos $k=2$, para $p=2$ dicho numero es compuesto pero para $p=3$ no lo es...

Encontrar todas las soluciones $(x,y)$  en enteros positivos para la ecuación $7^x-3\cdot 2^y=1.$
 

Sea $p$ un un entero positivo. El número $11p$ está compuesto de $m$ dígitos todos iguales a 1. Encontrar todos los valores de $m$ para los cuales $p$ es primo.

Sea $ n $ un entero positivo. Una baraja de $2n$ cartas contiene exactamente dos cartas marcadas con cada uno de los enteros $1,2,\ldots,n.$  Las cartas se ordenan en la forma $1,1,2,2,3,3,...,n,n.$  La baraja ya ordenada de esta manera se parte, y resulta que, en las dos partes, los dígitos en las cartas suman la misma cantidad.

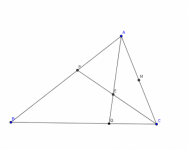
Sea ABC un triangulo, M el punto medio de CA, P el punto donde la bisectriz desde C intersecta a AB; E y Q son los puntos donde una ceviana desde A intersecta a la bisectriz y al lado BC, respectivamnete (Q no esta en la prolongacion de BC). Demuestra que los segmentos PQ y CQ son iguales, si y solo si B, E y M son colineales.

El Chico Fresa recién regresó de Italia y les trajo cuadernos a sus cuates. ¿De cuántas formas puede distribuir los 15 Moleskine entre 4 de sus amigos, bajo la condición de que a Baldo le toquen al menos 3, a Carlos al menos 2 y a Daniel al menos 1? (Nota: a Eulogio le puede tocar cualquier número --lo siento el chico fresa tiene sus preferidos.)

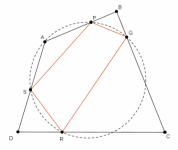
Sea ABCD un cuadrilátero para el cuál existen cuatro puntos P, Q, R y S sobre los lados AB, BC, CD y DA respectivamente y tales que PB=BQ, QC = CR, RD = DS y  SA = AP. Demuestra que:

• a) El cuadrilátero ABCD es circunscrito
• b) El cuadrilátero PQRS es cíclico.

¿De cuántas formas se pueden acomodar en línea recta siete pelotas blancas y cinco negras, de tal manera que no estén dos pelotas negras juntas?

Sean ABC un triángulo isósceles rectángulo en A, J su incentro y AD, BE las bisectrices de los ángulos A y B, respectivamente. La altura AD es tangente al incírculo del triángulo ADC (con incentro en I) en P y al lado CA en Q. Demostrar que:

Sean $a$ y $b$ enteros positivos de 8 dígitos cada uno, tales que al quitar cualquier dígito de $a$ (pero solo uno) y colocar el correspondiente en posición con $b$, se cumple que el número formado es divisible entre 7 (en cualquiera de los 8 posibles cambios). Demuestra que $b$ es divisible entre 7.