Intermedio
P1. OMM 1987. Suma de dos fracciones que dan entero
Consideremos dos fracciones reducidas ab y cd con b,d>0 . Si la suma de estas dos fracciones es un número entero entonces b=d.
Fermat converso (en general, espurio)
Demostrar que si p,q son dos primos distintos para los cuales ap≡a(modq) y aq≡a(modp), entonces apq≡a(modpq). }
Demostrar, con este resultado, el siguiente contraejemplo para la conversa del pequeño teorema de Fermat: 2340≡1(mod341) --¡pero 341 es compuesto!
Una factorización no trivial
Factorizar las siguientes expresiones algebraicas:
x4+6x3+11x2+6x+1
x4+6x3+11x2+6x
Genera un problema de concurso, en vista de las dos factorizaciones.
Residuo de un factorial (módulo un primo)
Encontrar el residuo que deja 50(50!) al dividirlo entre 53.
Inverso (mod 151) de una potencia de 2
Encontrar un número entero positivo que al multiplicarlo por 2145 y al resultado restarle 1, se obtenga un múltiplo de 151.
Expresable como combinación lineal
Decidir (con justificación) cuál de los tres números 2007,2008,2009 podría ser expresado como una combinación lineal entera de 453 y 408, es decir, en la forma 453x+408y, con x,y enteros.
Encontrar un residuo
Encontrar el residuo que deja 20092008 al dividirlo entre 9
Demostrar cuadrado
Sea ABCD un cuadrilatero tal que los angulos internos en los vertices A, B, y C son de cuarenta y cinco grados. Demostrar que los puntos medios de los lados del cuadrilatero determinan un cuadrado.
Propuesto por: Fernando
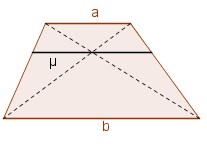
Media armónica de las bases de un trapecio.
Considere μ un segmento paralelo a las bases a y b de un trapecio, de tal manera que μ pasa por el punto de intersección de las diagonales y sus extremos están sobre los lados del trapecio. Demostrar que μ es la media armónica de a y b, es decir:
No es un cuadrado perfecto
Demostrar que si y es un entero, 187y−1 no es un cuadrado perfecto.
