Intermedio
Incentivo paternal
El padre quiere que su hija sea campeona en matemáticas de concurso. Le dice:"Por cada problema que resuelvas te daré 70 pesos y por cada uno que no resuelvas me darás 50 pesos." Después de intentar los n problemas de la lista que su papá le dio, la niña ha ganado 550 pesos. ¿Cuáles son los posibles valores de n?
Acertijo lógico con tres variables dicotómicas
El exitoso empresario X, rico de nacimiento, quiere contratar los servicios de un guardaespaldas para proteger su persona de la delincuencia organizada. Para ello habla con el director de la agencia Z, especializada en ese tipo de contrataciones.
XXIIIOMM Problema 3
Sean $a,b,c$ números reales positivos tales que $abc=1$. Muestra que
$ \frac {a^3}{a^3+2} + \frac {b^3}{b^3+2} + \frac {c^3}{c^3+2}\geq 1$ y que $ \frac {1}{a^3+2} + \frac {1}{b^3+2} + \frac {1}{c^3+2} \leq 1$
XXIIIOMM Problema 1
Sean ABC un triángulo y AD la altura sobre el lado BC. Tomando a D como centro y a AD como radio, se traza una circunferencia que corta a la recta AB en P, y corta a la recta AC en Q. Muestra que el triángulo AQP es semejante al triángulo ABC.
Construir un cuadrado inscrito a otro
Sean ABCD un cuadrado y M un punto en el interior de éste. Construir con regla y compás un cuadrado PQRS con sus vértices sobre los lados de ABCD y que M esté sobre alguno de los lados de PQRS.
Incentro y circuncírculo
Dado un triángulo $ ABC $, sea $I$ su incentro y $ L $ el punto donde la linea $ AI $ intersecta al circuncirculo . Demuestra que $ AL/LI=(AB+AC)/BC.$
Un problema de lógica
Cuatro miembros de la banda XYZ comían un día juntos en una fonda chiquita. Eran dos mujeres, La Buchona y La Gitana, y dos hombres, El Talibán y El Cochiloco. Cada uno tenía un oficio diferente: Burrero, Gatillero, Guardaespaldas y Oreja. (La mesa era cuadrada y para cuatro.) Con los siguientes datos encontrar el oficio de cada quien.
Eliminación con dos operaciones
En cada cuadrado de un tablero rectangular hay un entero positivo. Se pueden modificar los números del tablero usando alguno de los siguientes movimientos.
--Multiplicar por 2 cada número de un renglón.
--Restar 1 a cada número de una columna.
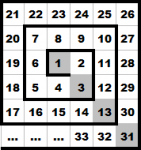
Números en espiral
Considera la sucesión $\{1,3,13,31,\ldots\}$ que se obtiene al seguir en diagonal el siguiente arreglo de números en espiral.
Encuentra el número en la posición 100 de esa sucesión.
Olimpiada Iberoamericana (el 4 de 2008)
Demuestra que no existen enteros positivos $x,y$ tales que $x^{2008}+2008!=21^y$
