Geometría
Áreas enteras de triángulos
El área del triángulo ABC es un entero. Sobre los lados BC y AC se eligen los puintos X y Y, respectivamente. Los segmentos AX y BY se cortan en un punto P dentro del triángulo ABC. El área de BPX es 1, la de APY es 2, y la de APB es un entero. Encontrar el área del triángulo ABC.
Segmentos iguales y colinealidad
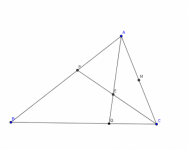
Sea ABC un triangulo, M el punto medio de CA, P el punto donde la bisectriz desde C intersecta a AB; E y Q son los puntos donde una ceviana desde A intersecta a la bisectriz y al lado BC, respectivamnete (Q no esta en la prolongacion de BC). Demuestra que los segmentos PQ y CQ son iguales, si y solo si B, E y M son colineales.
Cuadrilátero cícliclo dentro de un cuadrilátero circunscrito
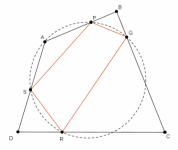
Sea ABCD un cuadrilátero para el cuál existen cuatro puntos P, Q, R y S sobre los lados AB, BC, CD y DA respectivamente y tales que PB=BQ, QC = CR, RD = DS y SA = AP. Demuestra que:
- a) El cuadrilátero ABCD es circunscrito
- b) El cuadrilátero PQRS es cíclico.
IMO4_2009_invertido
Sean ABC un triángulo isósceles rectángulo en A, J su incentro y AD, BE las bisectrices de los ángulos A y B, respectivamente. La altura AD es tangente al incírculo del triángulo ADC (con incentro en I) en P y al lado CA en Q. Demostrar que:
Equilátero seccionado (3G, take_home_1)
Sea ABC un triángulo equilátero y A’, B’ , C’, puntos sobre los lados BC, CA y AB, respectivamente, tales que AC′/C′B=BA′/A′C=CB′/B′A=2 Las intersecciones de los segmentos AA’, BB’ y CC’ determinan un triángulo interior, digamos, DEF.
Una propiedad trivial de la potencia de un punto
Sean dados tres puntos distintos O, P, Q en el plano. Demostrar que OP=OQ si y sólo si P y Q tienen la misma potencia respecto a un círculo cualquiera con centro en O.
IMO 2009 Problema 2
Sean ABC un triángulo de circuncentro O, P y Q puntos sobre AB y AC, respectivamente, y K, L, M los puntos medios de BQ, CP y PQ, respectivamente. Si el circuncírculo del triangulo KLM es tangente a PQ, demostrar que OP=OQ.
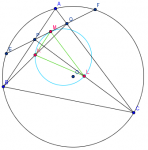
IMO 2009 Problema 4
En un triángulo ABC, donde AB=AC, los bisectrices internas de ∠A y ∠B cortan a los lados BC y AC en D y E, respectivamente. Sea I el incentro del triángulo ADC. Supongamos que ∠IEB=45. Encontrar todos los valores posibles de ∠A.

Probar isósceles
En una semicircuferenica de diámetro AB se elige un punto D y se baja una perpendicular al diámetro AB cortándolo en C. En el espacio descrito por DC, CB y el arco BD se inscribe un círculo tangente a CD en L, a BC en J y al arco BD en K. Demostrar que AD=AJ.
Potencia de un punto y circunferencias ortogonales
Sean dados una circunferencia c de radio r y centro O, y dos puntos M y M' tales que OM⋅OM′=r2 (i.e., inversos uno del otro respecto a c). Demostrar que cualquier circunferencia c' que pase por M y M' es ortogonal a c.
