Geometría
XXIIIOMM Problema 5
Considera un triángulo ABC y un punto M sobre el lado BC. Sea P la intersección de las perpendiculares a AB por M y a BC por B, y sea Q la intersección de las perpendiculares a AC por M y a BC por C. Muestra que PQ es perpendicular a AM si y sólo si M es punto medio de BC.
XXIIIOMM Problema 1
Sean ABC un triángulo y AD la altura sobre el lado BC. Tomando a D como centro y a AD como radio, se traza una circunferencia que corta a la recta AB en P, y corta a la recta AC en Q. Muestra que el triángulo AQP es semejante al triángulo ABC.
Construir un cuadrado inscrito a otro
Sean ABCD un cuadrado y M un punto en el interior de éste. Construir con regla y compás un cuadrado PQRS con sus vértices sobre los lados de ABCD y que M esté sobre alguno de los lados de PQRS.
Incentro y circuncírculo
Dado un triángulo ABC, sea I su incentro y L el punto donde la linea AI intersecta al circuncirculo . Demuestra que AL/LI=(AB+AC)/BC.
IX Olimpiada Norestense de Matemáticas (Problema 3)
El incírculo del triángulo △ABC es tangente al lado AB en el punto P y al lado BC en el punto Q. El círculo que pasa por los puntos A,P,Q corta por segunda vez a la recta BC en M y el círculo que pasa por los puntos C,P,Q corta por segunda vez a la recta AB en el punto N.
XXIV Olimpiada Iberoamericana de Matemáticas (problema 4)
Sea ABC un triángulo con AB≠AC. Sean I el incentro de ABC y P el otro punto de intersección de la bisectriz exterior del ángulo A con el circuncírculo de ABC. La recta PI intersecta por segunda vez al circuncírculo de ABC en el punto J. Demostrar que los circuncírculos de los triángulos JIB y JIC son tangentes a IC y a IB, respectivamente.
XXIV Olimpiada Iberoamericana de Matemáticas (problema 3)
Sean C1 y C2 dos circunferencias de centros O1 y O2, con el mismo radio, que se cortan en A y en B. Sea P un punto sobre el arco AB de C2 que está dentro de C1. La recta AP corta a C1 en C, la recta CB corta a C2 en D y la bisectriz del ∠CAD intersecta a C1 en E y a C2 en L. Sea F el punto simétrico a D con respecto al punto medio de PE. Demostrar que existe un punto X que satisface ∠XFL=∠XDC=30∘ y CX=O1O2.
¿Trazo auxiliar? OK Pero... ¿cómo lo descubres?
En un triángulo isósceles AOB, rectángulo en O, se eligen los puntos P,Q,S en los lados OB,OA,AB, respectivamente, y un punto R interior al triángulo, de tal manera que el cuadrilátero PQRS sea un cuadrado. Si la razón de áreas entre el cuadrado y el triángulo es 2/5, calcular la razón OP/OQ.
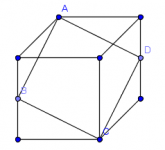
Cuadrilátero en un cubo
En un cubo de arista 6 los puntos medios B,D de dos aristas opuestas, y dos vértices opuestos A,C pero no en las aristas de los puntos medios B,D, forman un cuadrilátero ABCD. Encontrar el área de ese cuadrilátero.
Semicírculo y la descomposición en dos sumandos de un segmento.
Sea $$BC$ el diametro de una semicirculo y sea $A$ el punto medio del semicirculo. Sea M un punto sobre el arco $AC$. Seam $P$ y $Q$ los pies de las perpendiculares desde $A$ y C a la linea $BM$, respectivamente.
Demustra que BP=PQ+QC
