Geometría
Problema 1
El pentágono ABCDE es tal que AB=BC y CD=DE, y sus ángulos en A,C, y E son rectos. Encontrar la medida del ángulo ECA.
Encuentra el ángulo
El triángulo ABC es rectángulo en C, y las bisectrices de sus ángulos en A y B cortan los lados BC y CA en P y Q respectivamente. Los puntos M y N sobre el lado AB son los pies de las perpendiculares bajadas desde P y Q, respectivamente. ¿Cuánto vale el ángulo MCN?
Ptolomeo invisible
Se tiene inscrito en una circunferencia un 3n-agono regular, donde sus vertices son A1,A2,...,A3n Si se coloca un punto P de manera arbitraria sobre sobre la circunferencia, y desde P se trazan todas las rectas posible hacia todos los puntos Ai. Demostrar que: la suma de las n rectas trazadas mas grande, es igual a la suma de las 2n rectas mas pequeñas.
Gráfica de una ecuación
Discutir la ecuación xy=4y y, en particular, determina su gráfica.
Problema 7 (Ciudades, OMM_Tam_2010)
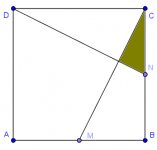
Sea ABCD un cuadrado con lado 1 cm. Si M y N son los puntos medios de los lados AB y BC, respectivamente. Calcular el área de la zona sombrada.
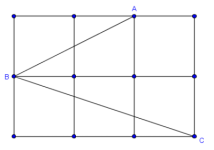
Problema 4 (Ciudades, OMM_Tam_2010)
La figura muestra una cuadrícula formada por 6 cuadrados. ¿Cuanto mide el ángulo CBA?
Cuadrilátero completo y puntos medios de sus diagonales
Consideremos a, b, c y d cuatro rectas no tres de ellas concurrentes (es decir, un cuadrilátero completo) y no dos de ellas paralelas. Demuestra que son colineales los puntos medios de las tres diagonales del cuadrilátero completo.
Nota: Las diagonales de un cuadrilátero completo son los segmentos que unen un punto de intersección de dos de sus lados con el de los otros dos lados.
Un punto en el interior de un triángulo
Sean P un punto en el interior del triángulo ABC y un ángulo α dado. Los ángulos en la base AB del triángulo ABP miden x y 90−2α, los ángulos en la base BC del triángulo BCP miden 90−2α y 2α−60, y los de la base CA del triángulo CAP miden 60+α y T. Encontrar el valor de x en términos de α. (¿Qué condiciones debe cumplir el valor α.)
Isósceles y equilátero --elemental pero no trivial
Sean ABC un triángulo, con AB=AC y ángulo en A de 100 grados, y un punto B' en el mismo plano de tal manera que AB'C es equilátero. Encontrar el ángulo ABB'.
Ejercicio 3.3.9
Sean π1,π2,π3,π4,π5,π6 tres planos en un espacio proyectivo tridimensional de tal manera que cada uno de los siguientes conjuntos de tres planos tienen una línea común de intersección:
{π1,π2,π3},{π1,π4,π5},{π3,π5,π6},{π2,π4,π6}
Más aun, no cuatro de éstos planos tienen una línea común.
Prueba que los seis planos tienen un punto en común.
