Geometría
Circunferencias con relación de radios
Sean C1 y C2 dos circunferencias tangentes externamente en S tales que el radio de C2 es el triple del radio de C1. Sea l una recta que es tangente a C1 en P y tangente a C2 en Q, con P y Q distintos de S. Sea T el punto en C2 tal que TQ es diámetro de C2 y sea R la intersección de la bisectriz de ∠SQT con el segmento ST. Demuestra que QR=RT
Punto exterior a un cuadrado
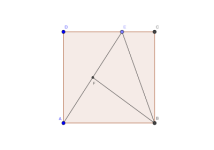
Sea ABCD un cuadrado. P un punto sobre la semicircunferencia de diámetro AB exterior al cuadrado. Sean M y N las intersecciones de PD y PC con AB, respectivamente. Demuestra que MN2=AM⋅BN
Cíclico dentro de un isóceles
Sea ABC un triángulo con AB=AC de gravicentro G. M y N los puntos medios de AB y AC respectivamente y O el circuncentro del trángulo BCN. Muestra que MBOG es un cuadrilátero cíclico.
Geometría del Primer Selectivo 2016
Sea ABCD un cuadrilátero cíclico y E y F puntos sobre la recta AB pero fuera del segmento AB con A entre E y B y B entre A y F. Demuestra que si ∠BED=∠AFC=∠DAC entonces EA=BF.
Problema 3 - IMO 2016 - Área de un polígono cíclico de coordenadas enteras.
Sea P=A1A2…Ak un polígono convexo en el plano. Los vértices A1,A2,…,Ak tienen coordenadas enteras y están sobre un círculo. Sea S el área de P. Los cuadrados de las los lados de P son todos divisibles por un entero dado n. Demuestra que 2S es divisible por n,
Traducido del inglés.
Problema 1 - IMO 2016 - Concurrencia de rectas
El triángulo BCF tiene ángulo recto en B. Sea A el punto en la línea CF tal que FA=FB y F se encuentra entre A y C. El punto D está elegido de tal manera que DA=DC y AC es la bisectríz de ∠DAB. El punto E es tal que EA=ED y AD es la bisectríz de ∠EAC. Sea M el punto medio de CF. Sea X el punto tal que AMXE es un paralelogramo (donde AM∥EX y AE∥MX). Demuestra que las líneas BD, FX y ME son concurrentes.
Traducido del inglés.
Circunferencia tangente a un cateto
Sea ABC un triángulo rectángulo con ∠ABC=90, BC=72, AC=78. Se considera un punto D sobre el lado AB de tal modo que 2AD=BD. Sea O el centro de la circunferencia que pasa por los puntos A y D y es tangente al lado BC. Encuentra la medida del segmento OB.
Medida de segmento para área 2016
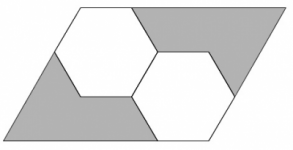
La región complemento de dos hexágonos
En la siguiente figura tenemos dos hexágonos con sus lados iguales. El paralelogramo tiene área de 2016 u2 , ¿cuál es el área de la región sombreada?
Escalinata
Sea △ABC un trinagulo isósceles con AC=CB,AB=7 y altura CD=9. Los segmentos a,b,c,d,e,f,g,h e i son paralelos a AB y dividen a CD en 9 segmentos iguales.
Encuentra a+b+c+d+e+f+i
