Problemas - Teoría de números
Solución de congruencias potenciales
Sea $a$ un entero positivo, coprimo con un primo $p$. Analizar la ecuación de congruencias $x^n \equiv a \pmod{p}$ en cuanto a sus posibles soluciones.
Raíces primitivas de un primo: una propiedad logarítmica
Sean $p$ un número primo y $g$ una de sus raíces primitivas. Demostrar que dos enteros positivos $i,j$ son equiresiduales en la división entre $p-1$ si y sólo si $g^i,g^j$ son equiresiduales en la división entre $p$
Par o impar --esa es la pregunta
Si $m$ y $ n $ son números impares ¿qué se puede decir de $(m-1)(n^2-1)/8$? Justifica tu respuesta.
Vieta en descenso infinito
Considere el cociente $k$ que resulta de dividir $x^2+y^2+1$ entre $xy$, con $x,y$ enteros positivos y la división tiene residuo cero. Determine todos los valores enteros posibles de $k$.
Magia con matemáticas
Sea $ K $ un entero positivo de $ n $ cifras y $ S $ la suma de todas las cifras de $ K $. Demuestra que $ K $ menos $ S $ es múltiplo de 9 para todo $ n $, con $ n $ mayor o igual a 2.
Un acertijo de Lewis Carroll
Varios escuelantes se sientan formando un círculo de manera que cada uno tiene dos vecinos, y quedan en un orden tal que el primero tiene un dollar más que el segundo y éste tiene un dollar más que el tercero, etc.
Incentivo paternal
El padre quiere que su hija sea campeona en matemáticas de concurso. Le dice:"Por cada problema que resuelvas te daré 70 pesos y por cada uno que no resuelvas me darás 50 pesos." Después de intentar los n problemas de la lista que su papá le dio, la niña ha ganado 550 pesos. ¿Cuáles son los posibles valores de n?
Múltiplos de 11
Encontrar todos los números de tres cifras múltiplos de 11 , y tales que la suma de sus dígitos es 10, y la diferencia entre el número y el que resulta al invertir sus dígitos es 297.
Números en espiral
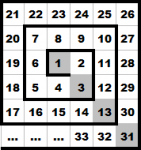
Considera la sucesión $\{1,3,13,31,\ldots\}$ que se obtiene al seguir en diagonal el siguiente arreglo de números en espiral.
Encuentra el número en la posición 100 de esa sucesión.