Publicaciones Recientes
Torres de Hanoi: un ejemplo de juego reglado
Las Torres de Hanoi es un acertijo matemático que consiste de tres postes y varios discos de diferente diámetro con un orificio central, de manera que se puedan ensartar en los postes. Es un juego reglado --muy útil para adquirir la disciplina de jugar de acuerdo a unas reglas... y para otras proficiencias en el problem solving.

Ptolomeo invisible
Se tiene inscrito en una circunferencia un 3n-agono regular, donde sus vertices son $A_{1},A_{2},...,A_{3n}$ Si se coloca un punto $P$ de manera arbitraria sobre sobre la circunferencia, y desde $P$ se trazan todas las rectas posible hacia todos los puntos $A_{i}$. Demostrar que: la suma de las n rectas trazadas mas grande, es igual a la suma de las 2n rectas mas pequeñas.
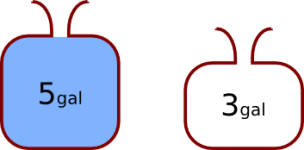
Duro de Matar y el problema de las jarras de agua.
En este post presento un video con el fragmento de la película de Duro de Matar donde aparece el problema de las jarras de agua. Y poteriormente, daré una solución a ese problema.
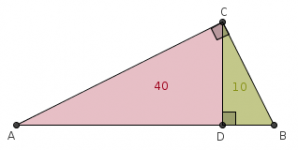
Relación entre la razón de semejanza y la razón de áreas
Inspirado por la solución de Luis Germán al Problema 7 (Ciudades, OMM_Tam_2010) decidí escribir este post. En su solución, Luis Germán usa un resultado conocido pero que pocos se dan cuenta de su importancia. Este resultado, aunque elemental, permite atajar muchísimo la solución a algunos problemas. Con este resultado, Germán pudo calcular el área del triángulo en cuestión sin tener que calcular todos sus lados.
Arma Mortal
Mel Gibson es 4 años mayor que su ex-esposa Robyn. Hace 6 años la edad de Mel era el doble que su vida de casado con Robyn. Si no se hubieran divorciado el año pasado, este año ella habría cumplido 3/5 de su edad casada con Mel. ¿Cuántos años tienen?
Máximo con restricciones
Los números reales $a,b,c,d,e$ suman 8 , sus cuadrados 16. Encontrar el máximo valor que puede obtener $e$.
Razonar la representación decimal de un número
Un número de 4 dígitos es 9 veces el número que resulta de quitarle el primer dígito. Encontrar todos los valores posibles de ese primer dígito.
Suma de consecutivos
La suma de 18 enteros consecutivos positivos es un cuadrado perfecto. Encontrar el mínimo valor que puede tener esa suma.
¿Qué es lo que no se puede hacer con los primos?
Encontrar todos los valores enteros positivos $ n $ para los cuales $f(n)=n^2-3n+2$ es un número primo. Justifica tu respuesta.
Trasquilar la borrega... ¿te hace sentido?
Seguramente la frase "trasquilar la borrega" no te hace sentido pero... quizá al terminar de leer este post le puedas atribuir un sentido...
Este domingo que pasó me desperté con la idea de ponerme a escribir un post para MaTeTaM sobre el último grito de la moda en educación matemática o, mejor dicho, en didáctica de las matemáticas (por lo menos en USA), denominado reasoning and sense making, pues entre semana había navegado un poco en la Web investigando sobre la guerra de las matemáticas (Math Wars) en Estados Unidos.
