Publicaciones Recientes
Problema 5, IMO 2010
En cada una de las seis cajas B1,B2,B3,B4,B5,B6 hay inicialmente sólo una moneda. Se permiten dos tipos de operaciones:
- Tipo 1: Elegir una caja no vacía Bj , con 1≤j≤5. Retirar una moneda de Bj y añadir dos monedas a Bj+1.
- Tipo 2: Elegir una caja no vacía Bk, con 1≤k≤4. Retirar una moneda de Bk e intercambiar los contenidos de las cajas (posiblemente vacías) Bk+1 y Bk+2.
Determine si existe una sucesión finita de estas operaciones que deja a las cajas B1,B2,B3,B4,B5 vacías y a la caja B6 con exactamente 201020102010 monedas. (Observe que abc=a(bc).)
Problema 2, IMO 2010
Sea ABC un triángulo, I su incentro y Γ su circunferencia circunscrita. La recta AI corta de nuevo a Γ en D. Sean E un punto en el arco ^BDC y F un punto en el lado BC tales que
∠BAF=∠CAE<12∠BAC.
Sea G el punto medio del segmento IF. Demuestre que las rectas DG y EI se cortan sobre Γ.
Problema 4, IMO 2010
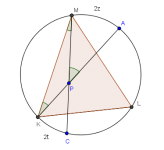
Sea P un punto en el interior del triángulo ABC con circunferencia circunscrita Γ. Las rectas AP,BP,CP cortan otra vez a Γ en los puntos K,L,M, respectivamente. La recta tangente a Γ en C corta a la recta AB en S. Demostrar que si SC=SP entonces MK=ML.
Problema 1, IMO 2010
Determine todas las funciones f:R→R tales que f(⌊x⌋y)=f(x)⌊f(y)⌋ para todos los números x,y∈R. (⌊z⌋ denota el mayor entero que es menor o igual que z.)
Sentido de la estructura geométrica
Chicas Fresa en Palacio
Las chicas fresa andan en Palacio de Hierro (sólo les faltan los lentes para irse de vacaciones a Los Cabos):
K: "¿Ya vieron? ¡Qué looser! ¡Son piratas! Nada que ver conmigo, yo quiero unos Carrera, Champion como los de Lady Gaga".

IMO 2010: México lugar 33
Después de que el año pasado la delegación mexicana que acudió a la Olimpiada Internacional de Matemáticas (IMO por sus siglas en inglés) se derrumbó hasta el lugar 50, en la IMO 2010 obtuvo el lugar 33 como país (con una plata y tres bronces), regresando a un nivel satisfactorio. (En los últimos 10 años, los lugares de México en la IMO han sido: 33 (2010), 50, 37, 24, 31, 37, 41, 46, 46, 32(2000).
P6 OMM 2001. Cuatro axiomas para colección de monedas
Un coleccionista de monedas raras tiene monedas de denominaciones 1,2,3,…,n (tiene muchas monedas de cada denominación). Desea poner algunas de sus monedas en las cajas de manera que se cumplan las siguientes condiciones:
P5 OMM 2001. Probar isósceles... ¿cómo se prueba isósceles?
Sea ABC un triángulo tal que AB<AC y el ángulo BAC es el doble del ángulo BCA. Sobre el lado AC se toma un punto D tal que CD=AB. Por el punto B se traza una recta l paralela a AC. La bisectriz exterior del ángulo en A intersecta a l en el punto M, y la paralela a AB por C intersecta a l en el punto N. Prueba que MD=DN.
P4 OMM 2001. Lista de residuos cuadráticos
Dados dos enteros positivos n y a, se forma una lista de 2001 números como sigue:
- el primer número es a;
- a partir del segundo, cada número es el residuo que se obtiene al dividir al cuadrado del anterior entre n.
A los números de la lista se les ponen los signos + y −, alternadamente
empezando con +. Los números con signo así obtenidos se suman, y a esa suma se le llama suma final para n y a.
¿Para qué enteros n≥5 existe alguna a tal que 2≤a≤n/2, y la suma final para n y a es positiva?
