Intermedio
Dígitos finales, problema casi ateorico
Encontrar el entero positivo n más pequeño para el cual los últimos tres dígitos de 2007n (en la notación usual de base 10) son 837.
divisibilidad y division de polinomios
Encontrar todos los enteros positivos n distintos de la unidad para los cuales la expresión (n3−1)/(n2+7n−8) es un entero.
Ubicación del ortocentro con una sola altura
Sean AB cuerda de una circunferencia y P un punto en AB tal que AP=2PB. Sea DE la cuerda perpendicular a AB que pasa por P. Demostrar que el punto medio Q de AP es el ortocentro del triángulo ADE.
El mulo y la burra generalizado (Problema 4, regiones 2008)
Abel le dice a Bárbara: si me dieras n yo tendría dos veces lo que a ti te quede. Bárbara le contesta: si tú me dieras 2 yo tendría n veces lo que a ti te quede. Encontrar todos los valores enteros positivos posibles de n.
Longitud Mínima
Sea ABC un triángulo y P un punto que se mueve sobre la recta que contiene al lado BC. Consideremos M y N los pies de las perpendiculares trazadas desde P sobre los lado AB y AC respectivamente. Encuentra el punto P para el cual MN tiene longitud mínima.
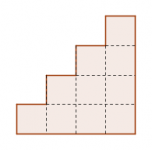
P4 OMM 2006. Zacatecas 2006: n-cubrimiento de una n-escalera
Como se sabe, en problemas de olimpiada, el enunciado puede tener una trampa de significado. El problema 4 del XX concurso nacional de la Olimpiada Mexicana de Matemáticas consiste de una pregunta “para qué enteros…”. La mayoría de los concursantes respondieron a la pregunta. Pero a la hora de las revisiones se supo que no bastaba con decir “estos son” sino que había que demostrar que no había otros. La solución necesitaba estar en el formato “los enteros n cumplen la condición si, y sólo si, son de la forma n = f(k)”. He aquí el enunciado del problema 4 del concurso nacional de 2006.
Un teorema sobre primos
Para todo primo p, si p2+2 es primo entonces p3+2 es también primo.
Ternas Pitagóricas
Demuestre que para cualquier terna pitagórica a2+b2=c2, alguno de los números a,b,c es divisible por tres.
Longitud mínima - caso particular
Sean ABC un triángulo rectángulo en A, y P un punto móvil en la hipotenusa BC.
Método "Busca donde hay luz"
Encontrar todas las tripletas de enteros (a,b,c) tales que el producto de dos de ellos más el tercero sea la unidad (o sea el 1).
