El día de hoy 25 de noviembre de 2013 inició la XXVII Olimpiada de Matemáticas en Huasca, Hidalgo. Los jóvenes participantes intentaron resolver (y seguramente varios lo lograron) 3 problemas en un lapso de 4 horas y media.

Cada selección estatal consta de 6 adolescentes (los más cabecillas de su estado). Según información del Delegado Tamaulipas para la OMM, el examen del primer día estuvo difícil --según los comentarios de pasillo de la selección Tamaulipas y quizá de otras.

En este post voy a continuar el post anterior sobre vectores añadiendo dos operaciones adicionales a las ya abordadas (suma y resta y multiplicación por un escalar).

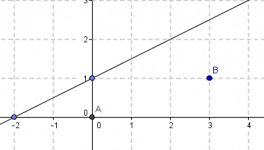
Se trata del producto interior (o escalar o punto) entre dos vectores y el producto área (o exterior o cruz), los cuales aportan, respectivamente, sendos criterios para la perpendicularidad y la colinealidad de vectores. Se discuten algunas instancias de uso para demostrar el potencial de los vectores en el problem solving de geometría. Voy a iniciar con un

Como se sabe, el número de subconjuntos de tamaño $k$ tomados del conjunto $\{1,2,\ldots,n\}$ se calcula con la fórmula

Puesto que este post es sobre argumentos combinatorios, empezaremos con la derivación de la fórmula de las combinaciones.

Dos modelos generales de razonamiento combinatorio

Modelo de la urna: los n objetos están dentro de una urna y se eligen k en sucesión y sin reemplazo.

En el concurso estatal de la XXVII OMM Tamaulipas 2013, el problema 4 fue de álgebra y la expectativa era que nadie lo resolvería. Pero, para nuestra sorpresa, un alumno del CBtis 15 (el plantel sede) lo resolvió correctamente (usando derivadas). Vaya una felicitación para Oscar Rosas Castillo por no dejarse intimidar por ese problema --y por tener las herramientas necesarias para resolverlo.

El problema (y algunos comentarios)

4A. Encontrar el valor mínimo de la expresión $(x^4+x^2+5)/(x^2+1)^2$ y el valor de la $x$ para el cual se logra.

En este post voy a argumentar a favor del uso de los vectores en el problem solving en geometría. Con las definiciones iniciales de vector, vectores de posición, vectores libres, igualdad de vectores, y la suma y resta de vectores presento la demostración de varios teoremas de la geometría como instancias de uso de esta poderosa herramienta. Destacan las instancias de uso finales sobre la demostración puramente vectorial de la fórmula de Sylvester y de la Recta de Euler.

El examen 

Concurso Estatal OMM Tamaulipas 2013 (CBtis 15, Cd. Mante, 4 de octubre)

1C. ¿De cuántas formas se pueden elegir dos fichas, de las 28 de un juego de dominó, de tal manera que las fichas tengan un número en común? Por ejemplo, [0|2] y [2|6] tienen en común al 2. Y también,  [1|2] y [1|4] tienen en común al 1.

Nota: Las 28 fichas del juego de dominó son [0|0], [0|1], [0|2], [0|3], [0|4], [0|5], [0|6]; [1|1], [1|2], [1|3], [1|4], [1|5], [1|6]; etc.

2G. En el triángulo ABC, se elige un punto D en el lado BC de tal manera que CD=d. Si AC=AD=3d y BD=8d, calcular la longitud de AB en términos de d.

Como se sabe, el significado básico de mutación es cambio (mutar, mudar). Y, en genética, es una alteración en la información genética de un ser vivo que cambia las características de éste (respecto a las usuales mostradas por los individuos de su especie) y que es incorporable a los mecanismos de la herencia.

Desde la perspectiva de la teoría evolutiva, el mutante introduce la variedad en una población y, por tanto, la posibilidad de un cambio en ella. Es decir, la posibilidad de evolucionar.

El día de hoy viernes 27 de septiembre quedó decidida la selección Victoria de la OMM Tamaulipas 2013. El concurso se llevó a cabo en el COBAT 5 y consistió de 10 problemas de respuesta abierta con valor de 7 puntos cada uno . Los siguientes alumnos participarán en el concurso estatal a celebrarse el próximo viernes 4 de octubre en las instalaciones del CBtis 15 en Cd Mante Tamaulipas.

# NOMBRE DEL ALUMNO                      ESCUELA     CALIFIC.

Orlando Ochoa Castillo generosamente ha enviado a la Delegación Tamaulipas de la OMM el contenido de los entrenamientos de la selección Guanajuato. No los había puesto en MaTeTaM porque no sabía cómo --dado que están en formato PDF.

Los comparto ahora con los lectores de MaTeTaM (como es la intención expresa de Orlando) para que estén disponibles en la Web para quien quiera seguirlos por su cuenta y, en particular, para los (futuros) preseleccionados de Tamaulipas --para la segunda semana de octubre se definirán. El material --que incluyo en los atachados-- consiste de nueve sesiones y algunas tareas.

En su libro Introduction to geometry, Wong Yan Loi presenta el problema motivo de este post (y lo resuelve con geometría analítica). La redacción del enunciado está aquí ligeramente modificada y a la solución le he añadido explicaciones que Wong Yan Loi se ahorra. (Me gustaría ver una solución sintética de este problema. Si alguien la encuentra sería una buena obra que la compartiera con los lectores de MaTeTaM.)