Voy a presentar en este post una forma de demostrar la desigualdad de Titu Andreescu que recuerda los procesos de bootstraping utilizados en computación --y otras áreas de la ciencia. El término bootstrapping está inspirado --verosímilmente-- en Las Sorprendentes Aventuras del Baron de Munchausen. (Una serie de narraciones donde el héroe realiza tareas imposibles.) Atacho una traducción al español.

Germán    27  plata (corte en 35)

Alain     21  bronce

José Luis 16  bronce

Jesús     13  mención

El corte para los oros en 35 significa --leyendo entre líneas-- que el examen estuvo relativamente fácil. Y también que aún si Germán hubiera resuelto el 2 (con lo cual habría obtenido 33 puntos) de cualquier manera el oro le quedaba a 2 puntos de distancia.

A continuación el examen del segundo día de la XVIII Olimpiada Mexicana de Matemáticas que se está aplicando a los concursantes el día de hoy en Toluca.

Problema 4 de la XXVIII OMM Segundo Día. Toluca 2014
Problema 5 de la XXVIII OMM Segundo Día. Toluca 2014
Problema 6 de la XXVIII OMM Segundo Día. Toluca 2014

Hoy se aplicó el examen del primer día de la XVIII Olimpiada Mexicana de Matemáticas.

Aquí una foto de la selección Tamaulipas 2014.

A continuación los 3 problemas, comenta o deja tu solución en la página de cada problema:

El problema y la solución de Germán

La suerte fue echada el domingo 12 con el selectivo final y los dados muestran hoy los resultados. Tenemos selección y MaTeTaM felicita a sus integrantes:

Germán Puga Castillo        
Roberto Alain Rivera Bravo
José Luis Domínguez Rodríguez
Julio Cesar Sandoval de la Cruz
Roberto Llanos Hernández
Jesús Francisco Anaya González 

Vaya una felicitación muy especial para Jesús, un joven con mucho futuro en la olimpiada (podrá ir en 2015 y 2016) --bueno si, como me gustaría esperar,  no se estaciona en los bronces.... 

Los saluda

jmd

1. Los números del 1 al 28 se acomodan al azar en una cuadrícula de $4\times7$ (4 filas y 7 columnas, un número en cada cuadrito). A continuación se consideran los productos $P_1$ de todos los números en la primera fila, $P_2$ el de todos los números en la segunda fila y, de la misma manera, se obtienen $P_3$ y $P_4$. Demuestra que alguno de estos cuatro productos es múltiplo de 128.

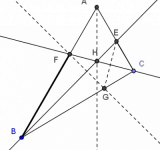
2. Sea K un punto sobre el arco AB del circuncírculo del triángulo isósceles $ABC$ (con AB=BC). Demuestra que

$$AK\cdot{KC}=AB^2-KC^2$$

En este post  voy a recomendar el estudio de algunos materiales sobre cuadriláteros cíclicos a quienes se están preparando para el nacional. De paso intercalo dos instancias de su uso.

En un post anterior --dedicado a los criterios de reconocimiento  de los cuadriláteros cíclicos-- hemos destacado la importancia de esta herramienta en el problem solving de geometría y discutimos varias instancias de uso asociadas a demostraciones del teorema de la mariposa.

Enseguida presento los cuatro problemas del segundo examen selectivo para la preselección Tamaulipas OMM 2014. Añado las soluciones al 2 y al 4.

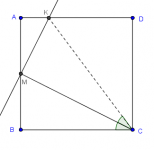
Problema 1. En un cuadrilátero ABCD convexo se trazan las perpendiculares desde cada vértice a la diagonal que no pasa por él. Demostrar que los cuatro puntos de intersección de cada perpendicular con su correspondiente diagonal forman un cuadrilátero semejante al dado.