Resultados de la OMM Tamaulipas etapa regional.
El dia de hoy, los seleccionados de la etapa municipal realizaron el segundo examen del proceso para pertenecer a la selección Tamaulipas 2016.
Presentaron en cuatro sedes: Reynosa,Victoria, El Mante y Madero. A continuación estan las actas de cada sede.
Los alumnos que aparezcan en estas actas estan seleccionados para participar en el concurso estatal a realizarse el 1 de julio de este año en las instalaciones de la UAM de Ciencias, Educación y Humanidades en Ciudad Victoria, Tamaulipas.
Los problemas los pueden consultar aquí mismo, ya estan arriba.
Saludos
Germán

Resultados de la OMM Tamaulipas etapa Municipal 2016
El pasado Viernes 20 de Mayo se realizó la etapa Municipal de la Olimpiada Mexicana de Matemáticas de Tamaulipas. Participaron más de 1200 estudiantes en 12 sedes.
Hasta el momento tenemos las actas con los resultados de 9 de las sedes. Los estudiantes que aparezcan en las listas podrán participar a la siguiente etapa (Etapa Regional) que se tiene programada para el próximo 3 de Junio.
¡Muchas felicidades a los ganadores!
P.D. Estamos en espera de los resultados de Victoria, González y Nuevo Laredo.
Actualización [22 de Mayo a las 14:02]: Ya actualizamos el acta de ganadores de Matamoros.
Resultados de la ONMAPS Tamaulipas 2016
El pasado viernes 14 de Mayo se llevó a cabo la Etapa Final de la Olimpiada Nacional de Matemáticas para Alumnos de Primaria y Secundaria (ONMAPS) de Tamauilpas. El examen se realizó en la Unidad Académica Multidiciplinaria de Ciencias, Educación y Humanidades de la UAT, ubicada en Cd. Victoria, Tamaulipas.
A continuación se enlistan los ganadores que representarán al estado en la etapa Nacional.
Prepárate para el municipal
Como saben, este Viernes 20 de Mayo será la primera etapa en nuestro proceso 2016.
El delegado Orlando ha enviado un examen de prueba para los que quieran conocer que tipo de problemas aparecerán el Viernes, al final lo adjunto.
También aprovecho para recordarles que aún se pueden inscribir para el concurso, llenando el formulario que se encuentra en el siguiente link:
https://docs.google.com/forms/d/1pi8UPeCY2HguynVcoHPfBi_jnmC1UTYvC-ojMYRWjNw/viewform?c=0&w=1
Los esperamos este Viernes :)
Saludos
germán
El nuevo delegado, la convocatoria y los premios.
Acaba de salir la convocatoria oficial (aprobada por la SEP y UAT) para participar en la Olimpiada Mexicana de Matemáticas (OMM) de Tamaulipas. No hay cambios mayores, las fechas, sedes y forma de inscripción son las mismas que ya habíamos mencionado.
Invitamos a todos los interesados a descargar la Convocatoria Oficial y el Cartel para que nos ayuden a difundir este evento que inicia el próximo 20 de Mayo. Los links de descarga los encontrarán al final de esta publicación.

Comienza el ciclo de la 30 Olimpiada Mexicana de Matemáticas en Tamaulipas

Jornadas en la Olimpiada de Tamaulipas
Para calentar motores antes de que inicie el proceso 2016, hemos (Orlando Ochoa, José Luis Medellin, Luis Javier Olvera,Roberto Alain y un servidor) diseñado un nuevo formato de competencia para los alumnos tamaulipecos que pueden volver a participar este año. Las llamadas ''Jornadas'' es una lista de problemas, que los alumnos realizan por equipos, y se evaluan dandoles puntos extras además de los 7 puntos por la solución de los problemas. Cada semana hay ganadores y una tabla de posiciones. La explicación del formato tal vez sea para después. Después de tres Jornadas, los problemas y soluciones más interesantes son los siguientes:
Jornada 1
Problema de Teoría de Números
Calendario Dodecaédrico con Origami 2016
Para hacer el calendario sólo tienen que descargar, imprimir, doblar y armar. Aquí está el video con las intrucciones de armado que hicimos para la versión 2010.
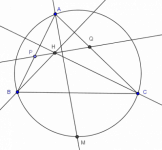
Sobre el problema 1 de la 29 OMM
El problema
Sea ABC un triángulo y sea H su ortocentro. Sea PQ un segmento que pasa por H con P en AB, Q en AC y tal que ∠PHB=∠CHQ. Finalmente en el ciruncírculo del triángulo ABC considera M el punto medio del arco BC que no contiene a A. Muestra que MP=MQ.
La solución
De acuerdo a los datos sobre la recta PQ que pasa por H, es fácil darse cuenta que PQ es bisectriz de los ángulos formados en H por las alturas.