Selección Tamaulipas 2015 y un examen muy difícil.
Preselección Tamaulipas OMM 2015
Enseguida se enlistan los 16 preseleccionados que se mantienen en la competencia para elegir la selección Tamaulipas OMM 2015.
Nombre Escuela Ciudad Puntaje
La dificultad de un problema depende del resolutor
En el presente post voy a presentar la solución de un problema de números que se me hizo realmente difícil y no lo pude resolver sin ayuda. Trato también de trasmitir a los lectores de MaTeTaM el modo de razonar de un experto en el problem solving de concurso. El problema es el siguiente:
Demostrar que, para todo entero no negativo k, 226k+2+3es múltiplo de 19.
Demostración (reconstruida a partir de una realizada por JRV en conversación telefónica con el que esto escribe)

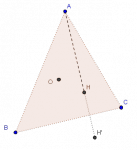
Sobre el ortocentro reflejado y el problema 3G
Creo que puede ser de alguna utilidad para los lectores de MaTeTaM la discusión de dos demostraciones del conocido teorema que dice:
El reflejo del ortocentro en el espejo de cualquier lado del triángulo pertenece al circuncírculo.
Una de ellas procede reflejando H en un lado (digamos BC) y demuestra que ese reflejo (digamos H′) pertenece al circuncírculo; la otra toma el punto H′ de intersección de la altura (digamos AH) con el circuncírculo y demuestra que H′ es el reflejo de H (en BC).
Resultados del concurso estatal Tamaulipas 2015
El concurso estatal de la Olimpiada Mexicana de Matemáticas Tamaulipas 2015 se celebró el viernes 28 de agosto en las instalaciones de la UAMCEH-UAT en Cd Victoria. Fueron 4 problemas de diversa dificultad los cuales se pueden ver en la sección de problemas de este sitio web.
El problema 1(A) fue el regalo para que nadie se sintiera mal. Pero a los participantes se les hizo muy difícil (según se puede ver por el número de ceros que recibió).
Un problema viral
Es bastante inusual que un problema de matemáticas de concurso llegue a la prensa diaria. Por ello es que me sorprendió que haya aparecido en El Universal el siguiente problema de matemáticas (aunque más bien es de lógica) en estos días de abril de 2015. (La nota decía, además, que el problema es de una olimpiada de Singapur --creo-- para niños de 14 años y se había vuelto viral en la WWW.)
Identidad notabilísima --y su determinante
Me he encontrado en estos días con la notabilísima identidad algebraica (para a,b,c reales):
abc+(a+b)(b+c)(c+a)=(a+b+c)(ab+bc+ca)
Su rasgo distintivo radica --creo-- en que el lado derecho refleja el izquierdo pero intercambiando la suma por el producto y éste por aquélla. Es decir, lo que en el lado izquierdo es producto en el derecho es suma y la suma en el izquierdo es producto en el derecho.
Seguir la regla y "ver como" en álgebra
Ahora que el 2014 se ha quedado atrás y el puente Guadalupe Reyes se terminó es buen momento para mirar hacia el futuro. Y desearle a toda la comunidad de usuarios de MaTeTaM un 2015 de eficaces aprendizajes en el problem solving de matemáticas.
Y, bueno, de paso voy a plantear la tesis de que, en el aprendizaje de las matemáticas, primero se aprende el procedimiento y sólo después de ello se aprende el concepto. Ilustro con un ejemplo de desigualdades.

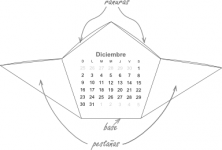
Calendario Dodecaédrico con Origami 2015
Para hacer el calendario sólo tienen que descargar, imprimir, doblar y armar. Aquí está el video con las intrucciones de armado que hicimos para la versión 2010.
Algunos de ustedes nos han comentado que les sobran muchas pestañas a la hora de armarlo. Les queremos decir que sí es posible armarlo sin pegamento y sin que sobren pestañas.
Riesgo moral y agencia --en educación superior
En este fin de 2014 en que la Academia de Ciencias sueca otorgó el premio Nobel de economía a Jean Tirole, puede que sea de alguna utilidad comentar sobre su enfoque (la Teoría de la Agencia) al analizar los mercados y su regulación. (Añado una discusión sobre la situación de la educación superior vista desde la perspectiva de esta importante teoría.)

