Geometría

Sea ABC un triangulo equilátero y R el radio de la circunferencia que lo circunscribe, demuestre que el area del triangulo es igual a:

En un triángulo acutángulo $ABC$, las alturas de $B$ y $C$ respecto a las bases $CA$ y $AB$, respectivamente, se intersectan en el punto $S$. Sean $M$ en $AB$ y $N$ en $CA$ los pies de esas alturas. Demostrar que $AB=CA$ si y sólo si el ángulo $MSB$ mide el doble que el ángulo $CBN$.

Si en un triángulo $ABC$ se construyen triángulos equiláteros interiores sobre sus lados, entonces los centros $X, Y, Z$ de dichos triángulos equiláteros determinan un triángulo equilátero $XYZ$, conocido como triángulo de Napoleón interior. (Demostrarlo.)

Si en un triángulo $ABC$ se construyen triángulos equiláteros exteriores sobre sus lados, entonces los centros $X, Y, Z$ de dichos triángulos equiláteros determinan un triángulo equilátero $XYZ$, conocido como triángulo de Napoleón exterior. (Demostrarlo.)
 

Dividir un segmento $AC$ en la razón $3/2$ (en razón de 3 a 2), internamente por un punto B y externamente por un punto $G$.

En la figura, los triángulos $ABC$ y $DEF$ son congruentes, con $BC=EF$. ¿Cuánto mide el ángulo EGC?

En el triángulo $ABC$, las alturas $CM$ y $BN$ se cortan en el punto $S$. Con los datos que se muestran en la figura, concluye que el triángulo es isósceles.

Si en un triángulo $ABC$ se toman los puntos $P$ en $BC$, $Q$ en $CA$ yR en $AB$, de tal manera que las rectas $QR, RP, PQ$ cortan a los lados $BC, CA, AB$ en los puntos $P', Q', R'$, res

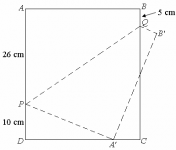
Una hoja de papel en forma rectangular $ABCD$ se dobla a lo largo de la línea $PQ$ de manera que el vértice $A$ quede en el lugar del punto $A’$ y el vértice $B$ en el lugar del punto $B’$. Al medir los segmentos $AP, BQ, DP$, se tiene que miden $26 cm, 5 cm$ y $10 cm$, respectivamente.

¿Cuál es el área del la hoja de papel?

En un rectángulo de base 10 y altura 8, se ha inscrito un paralelogramo de tal manera que en las esquinas del rectángulo se forman triángulos de catetos 4 y 7 y 3 y 4. Encuentra la distancia entre los lados opuestos del paralelogramo inscrito en el rectángulo.