Geometría
OMM 2008, Problema 6
Las bisectrices internas de los ángulos A, B y C de un triángulo ABC concurren en I y cortan
al circuncírculo de ABC en L, M y N, respectivamente. La circunferencia de diámetro IL,
corta al lado BC, en D y E; la circunferencia de diámetro IM corta al lado CA en F y G;
la circunferencia de diámetro IN corta al lado AB en H y J. Muestra que D, E, F, G, H,
J están sobre una misma circunferencia.
IMO 2008, Problema 1
Un triangulo ABC tiene ortocentro H. La circunferencia con centro en el punto medio de BC, que pasa por H, corta a la recta BC en A1yA2, de manera similar se definen los puntos B1,B2 en la recta CA y C1,C2 en la recta AB. Demuestra que los puntos A1,A2,B1,B2,C1,C2 estan en una misma circunferencia.
Problema 8 Geometrense
Sean ABC un triángulo y AP, AQ las tangentes desde A a la circunferencia de diámetro BC (P y Q los puntos de tangencia). Muestra que el ortocentro H de ABC está sobre PQ.
Perpendicular si y sólo si el triángulo es isósceles
Sea ABC un triángulo de circuncentro O, sea M el punto medio de AB y E el gravicentro del triángulo AMC. Demostrar que OE y CM son perpendiculares si y sólo si AB=AC
Perpendiculares
Para un triángulo ABC, toma los puntos M y N en las extensiones de AB y CB, respectivamente de tal manera que M y N estén más cerca de B que de A y C, y que AM=CN=s donde s denota el semiperímetro. Sea K el punto diametralmente opuesto a B e I el incentro del triángulo ABC.
Equilátero inscrito en equilátero
Inscribir un triángulo equilátero en un triángulo equilátero ABC, de tal manera que cada lado del inscrito sea perpendicular a un lado del triángulo ABC. (Describir el procedimiento de construcción.)
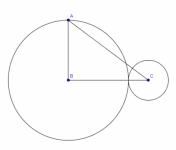
Problema 6G, Ciudades 2009
En la figura el segmento BC une los centros de los círculos tangentes, AB es perpendicular a BC,BC=8 , y AC=10. Calcular el área de cada círculo.
¿Incírculo o excírculo?
Sean D en AB y E en AC, los extremos de un segmento tangente al incírculo del triángulo ABC. Si los lados AB,BC,CA miden, respectivamente, c,a,b, expresar el perímetro del triángulo ADE en términos de a,b,c.
Medio rombo y un 30-60-90
Un rombo de lado 2m tiene un ángulo de 30∘. ¿Cuánto vale su área?
Inradio y cateto
Expresar el radio r del incírculo de un triángulo rectángulo isósceles en términos del cateto c.

