Geometría
El polo de la recta que pasa por el vértice y el punto de tangencia.
Sea ABC un triángulo y sean D, E y F los puntos donde la circunferencia circunscrita es tangente al lado BC, CA y AB. Llamemos D′ el punto donde la recta EF corta a la recta AB. Demuestra que:
a) D′ es el conjugado armónico de D con respecto al segmento AB.
b) Que la recta AD es la polar de D′ respecto al incírculo.
Demostrar cuadrado
Sea ABCD un cuadrilatero tal que los angulos internos en los vertices A, B, y C son de cuarenta y cinco grados. Demostrar que los puntos medios de los lados del cuadrilatero determinan un cuadrado.
Propuesto por: Fernando
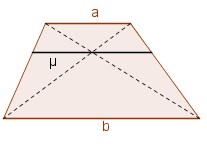
Media armónica de las bases de un trapecio.
Considere μ un segmento paralelo a las bases a y b de un trapecio, de tal manera que μ pasa por el punto de intersección de las diagonales y sus extremos están sobre los lados del trapecio. Demostrar que μ es la media armónica de a y b, es decir:
Tres círculos congruentes
Tres círculos C1,C2,C3 del mismo radio se intersectan no tangencialmente en un punto P. Sean A,B los centros de C1,C2, respectivamente; y C,D los puntos de intersección de C1,C2, respectivamente, con C3. (C,D son ambos diferentes de P.) Demostrar que ABCD es un paralelogramo.
Cíclico en tres circunferencias tangentes
Considere C1, C2 y C3 tres circunferencia que por pares son tangentes externas. Llamemos P y Q los puntos de tangencia de C1 con C2 y C3 respectivamente.
Problema de coolinealidad
Sean C1,C2,C3 tres circunferencias tangentes exteriores dos a dos. Definamos los siguientes puntos; R=C1∩C2 S=C1∩C3 y T=C2∩C3 , sean X,Y los puntos sobre C2,C3 de modo que XY sea la tangente comun y esta no pase por C1. Sea J la interseccion de la tangente a C1,C2 por R y a la tangente comun a C1,C3 por S.
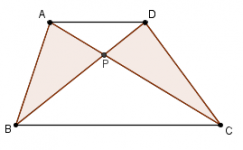
Áreas iguales en un trapecio
Demuestra que para cualquier trapecio ABCD, las áreas de las triángulos sombreados son iguales.
Producto de diagonales en un polígono regular
Sea A1,A2,…,An los n vértices de un polígono regular con circunferencia circuncrita de radio R, Demuestra que:
Isósceles semejantes sobre un triángulo
Consideremos A′, B′ y C′ tres puntos en el exterior del triángulo ABC, de tal manera que los triángulos A′BC, AB′C y ABC′ son todos isósceles semejantes y de bases BC, CA y AB respectivamente, Demuestra que AA′, BB′ y CC′ concurren.
Equiláteros en los lados de un triángulo
Este es un problema con la misma figura del triángulo de napoleón.
Consideremos los puntos A′, B′ y C′ puntos fuera del triángulos ABC de tal manera que los triángulos A′BC, AB′C y ABC′ son equiláteros. Demuestra que AA′, BB′ y CC′ concurren y son de la misma longitud.
